一
在我经过一番思索之后,我决定把目前英国哲学的观点作为我的出发点。因为我相信一位科学家或一位哲学家的职责是解决科学或哲学问题,而不是去谈论他或其他哲学家们正在做什么或可能做什么。任何解决科学或哲学问题的企图,如果它是诚实的而且是专心致志的,即使没有达到目的,在我看来,要比讨论“科学是什么”?或“哲学是什么”这类问题有意义得多。而且即使我们以较好的方式来提后一问题,即哲学问题是什么性质,拿我来说也不想多花功夫,我感到即使拿它和“每次讨论或评论是否总必须从不言而喻的‘假设’或‘假定’开始”这类次要的哲学问题相比,也是不重要的。
当把“哲学问题是什么性质”作为“哲学是什么”的较好形式来描述时、我想暗示当前关于哲学本质的争论是无益的,其一个理由就是天真地认为有所谓“哲学”或者“哲学活动”这样一个东西,它具有一定的性质、实质或‘本质’。认为物理学、生物学或者考古学,这些“研究”或“学科”,因它们研究的题材而有所区别,这种信念我认为是已往时代的遗留,那时候人们都以为一种理论必须从它自身的题材出发的。但是题材,或事物的种类,我认为并不构成区分学科的基础。学科的区分、部分地是由于历史的原因和行政管理的方便(有如教学和职位的组织)的原因,部分地是因为我们为了解决问题而建立的理论有一种发展为统一系统的趋向。但是所有这些分类和区别都是比较不重要的和浮面的。我们不是某些题材的研究者,而是某些问题的研究者。而问题可能冲破任何题材或学科的界限。
这个事实在某些人看来是很明显的,但因为对我们现在的讨论太重要了,值得用一个例子来说明它。一个地质学的问题,像估计某一城市有没有石油层或铀层贮存的可能性,必须借助于通常分为数学的、物理的和化学的理论和技术来解决,这是不需要指出的。然而,连一门更“基础”的科学,如原子物理学,在解决它的某一个最抽象和最基本理论时,如关于原子偶数序数或奇数序数的相对稳固性或不稳固性的试验预测的问题,可能要用到地质测量和地质理论与技术,那就不大明显了。
我完全准备承认,许多问题即使它们的解包含着许多不同的学科,在某种意义上仍然‘属于’这种或那种传统学科,如刚提到的两个问题就显然各自属于地质学和物理学。这是因为它们的讨论都与它们所牵涉到的学科的传统特性有关。它产生于某些理论的讨论,或起于有关某种理论的实验的讨论;而且理论与主题相反,是可以构成一门学科的(学科可以描述为一组不严格的理论经受着挑战,变化和成长)。但这并不影响我关于学科分类比较不重要的论点,而且我们研究的不是学科,而是问题。
但是有哲学问题吗?我认为,现在英国哲学的观点——我的出发点——起源于已故的维特根施坦教授的学说:他认为哲学问题是没有的;所有真正的问题都是科学问题;而所谓的哲学问题都是假问题;所谓哲学或理论命题都是假命题或假理论;它们并不是假的(假定它是假的,它的对立面将是真命题或真理论),而是严格说来是一些词的无意义的组合,不比一个还没有学会正常说话的小孩的不连贯的咿咿哑哑更有意义。
因此,哲学不能包含任何理论。按照维特根施坦的说法,它的真正性质不是一种理论,而是一种活动。一切真正哲学的任务是撕下哲学的无聊假面具,并教导人们如何谈论有意义的东西。
我的计划是把维特根施坦的学说作为我的起点。我将试图解释它(第2节),在某种程度上为它辩护,但又批评它(第3节)。我将用科学思想史的某些例子来说明这一切(从第4节到第10节)。
在进行这个计划以前,我想重申我确信一个哲学家应当进行哲学研究:他应试图解决哲学问题,而不应谈论哲学。如果维特根施坦的学说是真的,那么照我的说法,就没有人可以研究哲学了。如果这是我的见解,我将放弃哲学。但是碰巧我不但对某些哲学问题深感兴趣,(它是否“正确地”叫做‘哲学问题’,不去管它),而且希望对它的解决有所贡献——即使一点点也好,但是也要经过艰苦的工作。
二
自从黑格尔主义兴起以来,科学与哲学之间就存在着一条危险的鸿沟。哲学家被指摘为——或认为也是正当的不掌握事实知识而进行哲学论述;它们的哲学被描述为“只是幻想,甚至愚蠢的幻想”。虽然黑格尔主义在英国和大陆起了主导的作用,但它的对立面,以及对它的自命不凡的轻蔑,都从未完全熄灭。它的垮台是由一位哲学家造成的;这位哲学家像他以前的莱布尼茨、康德以及约翰 · 穆勒一样,这些哲学先就对科学特别是数学具有丰富知识。我讲的就是罗素。
维特根施坦的哲学理论是以陈述分类为基础的,而罗素也是陈述分类家(与他著名的类型论密切相关),罗素把语言的表达分为:
(1)真陈述
(2)假陈述
(3)无意义表述,其中有类似陈述的一串词语,可以叫做“伪陈述”。
罗素运用这种区分去解决他发现的逻辑悖论问题。为了解决他的问题,特别是(2)与(3)的区别尤为重要。在通常说话中,我们可以说,一个假陈述命题诸如‘3乘4等于173’或者‘所有的猫都是母牛’是无意义的。然而罗素都保留了‘无意义’这个术语,用于这样的表达,如‘3乘4是母牛’或‘所有的猫与173是等同的’,即是说用来指一种最好不作为假陈述的表述。这些最好不称为假陈述,因为有意义可言的假陈述一直是真的。但是伪陈述的有效否定“所有的猫等同173”是“有些猫不等同173”,而这作为一个伪陈述恰恰和原来陈述同样是不满意的。伪陈述的否定仍是伪陈述,正如正常陈述的否定(真或假)是正常陈述(相应地,伪或真)一样。
这个区别使罗素能于消除多种悖论(他说这些悖论是无意义的伪陈述)。维特根施坦更进一步。他或许由于有这样的感觉:不管什么哲学家,特别是黑格尔式的哲学家,他们说的话都类似逻辑悖论那样的话,因此他就用罗素的区别来谴责所有的哲学严格说来都是无意义的。
其结果是真正的哲学问题变得没有了。一切所谓哲学问题都可以分为四类:(1)那些纯逻辑或数学的,由逻辑或数学命题来回答,因而不是哲学的;(2)那些事实的,由属于经验科学的某些陈述来回答,因而也不是哲学的;(3)那些是(1)和(2)的结合,因而仍然不是哲学的;(4)无意义的假问题如“所有的猫等于173吗?”或者“苏格拉底是同一的吗?”或者“一个看不见的,摸不着的以及显然完全不能认识的苏格拉底存在吗?”
维特根施坦借助于罗素的类型论而根除哲学(和神学)的思想是有其创见的(甚至比孔德的实证主义更激烈,孔德的实证主义与之很相似)。这个思想成了学术界颇有势力的现代语言分析学派的灵感泉源。他们继承了他关于没有真正哲学问题的信念,认为哲学家所能做的只是揭露和消除传统哲学所提出的语言之谜。
我自己对这个问题的看法是,只要我有真正的哲学问题要解决,我将继续对哲学感到兴趣。我不理解哲学没有问题还会有吸引力。当然,我知道许多人在胡说,但应揭露这种胡说,因为它可能是很危险的胡闹,这将是一种任务(虽则是不愉快的任务),这是可以想象到的。但是我相信有些人曾经讲过某些不大有意思的话,而且的确也不大合乎文法,但却相当有道理和令人兴奋,或许比别人很有意思的话还要值得听取得多。我可以指出微分和积分,特别是它的早期形式,根据维特根施坦的标准,无疑是完全自相矛盾的和胡说八道的,然而,经过几百年人们在数学上伟大努力的结果,终于把基础建立起来了,但它的基础理论直到现时现刻还需要继续澄清,而且正在澄清。在这一点上,我们或许可以记起,给维特根施坦的早期追随着以深刻印象的,就是数学的表面绝对精确性和哲学语言的含糊性和不精确性之间的对比。但是如果当年有个维特根施坦运用他们的武器来反对微积分的先驱者,而且成功地消除那些胡说,而这是他们当代的批评者(有如贝克莱,他基本上是正确的)没能做到的,那么他当时就扼杀掉思想史上最有魅力和哲学上的最重要的一个发展。维特根施坦曾经写道:“一个人不能说话,那就只好沉默。”如果我没有记错的话,埃尔温 · 薛定谔曾经回答道:‘但是就是在这时说话才是有价值的’。微积分的历史——或许还有薛定谔自己的理论——都证实了他的说法。
毫无疑问,我们全都应该训练自己尽可能把话说得清楚、精确、简明、直接。然而我认为没有一本科学的或数学的名著,或一本的确值得阅读的书,经过语言分析技巧的巧妙应用,不能表明它含有许多无意义的假命题,有些也许可以把它叫做“套套逻辑”。
而且,我认为连维特根施坦采用罗素的理论就是根据一种逻辑错误。从现代的逻辑看来,在普通自然发展语言(相对于人工计算)范围内,只要遵守习惯和文法的约定规律,就没有理由谈什么假陈述或类型错误或范畴错误。人们甚至可以说,实证主义者以发难者自居,说我们使用无意义的词,或者我们在胡说八道,事实上就不知所云——他只是简单地重复从别人那里听来的而那人也不知道自己讲些什么。但这引起了一个技术问题,在这里无法论述了。(但在下面第11和12章,将讨论这个问题)。
三
我曾答应为维特根施坦的观点辩护几句。我想说的是,首先,有许多哲学著作(特别是黑格尔学派)恰恰可以作为无意义的冗辞来批判;其次,这类不负责任的文章,至少在一段时间内受到维特根施坦和语言分析家的影响而有所收敛(在这方面,最健康的影响是罗素的例子,他通过自己文章的无比魅力和清晰,建立了细致内容与清新和质朴风格的一致)。
但我准备再多讲一点。为了部分地为维特根施坦的见解辩护,我打算说明以下两个论题。
我的第一个论题是,每一种哲学,特别是每一哲学'学派',都会堕落到这种地步,使它的问题实际上与假问题无所区别,而它的术语实际上也就与无意义的胡言乱语无所区别。我将试图表明,这是哲学上近亲繁殖的结果。哲学学派的衰退又是起于一种错误的信念,即认为哲学的研究不需要哲学以外的问题的推动,例如数学、天文学、政治学、宗教或者社会生活中的问题。换句话说,我的第一个论题就是这样。真正的哲学问题总是植根于哲学以外的那些迫切问题,这些根烂了,哲学也随之死亡了。在解决这些问题的努力中,哲学家们常会追求一种看来像是哲学方法或技巧,或是解决哲学问题的金钥匙。但是这样的方法或技巧是不存在的;在哲学上,方法是不重要的;任何方法,只要能导致能够合理讨论的结果,就是正当的方法。要紧的不是方法或者技巧,而是对问题的敏感性,和对问题的一贯热情,或者,如希腊人说的,是惊奇的本性。
有些人感到解决问题的迫切要求,他们把问题看成是实在的东西,就像从他们的机体内非排除掉疾病一样。即使他们把自己局限于研究一种特殊方法或特殊技巧,他们也可以作出贡献。但是另外一些人并不感到这种迫切要求,他们并没有什么重大的、迫切的问题要解决,然而照旧运用流行的方法作些练习,对于他们说来,哲学是应用(你所合意的见解和技能)而不是探索。他们把哲学引入假问题和语言谜语词的泥沼;他们或者为我们提供假问题以代替真问题(维特根施坦所见到的危险),或者说服我们集中力量去揭露他们真正地或者错误认为的假问题或谜语;一种无休止的和不得要领的工作(维特根施坦所陷入的陷阱)。
我的第二个论题是,看来所谓讲授哲学的有效方法常会产生符合维特根施坦所描述的那种哲学,我所说讲授哲学的有效方法,以及看来是唯一的方法,就是给初学者(这些初学者我们认为并不懂得数学史、宇宙学史以及其他科学的思想和政治思想)阅读一些大哲学家的著作,譬如说柏拉图和亚里士多德,笛卡儿和莱布尼茨、洛克、贝克莱、休谟、康德和穆勒的著作。这样一个阅读课的效果是什么?在读者面前展现了一幅惊人的微妙而广大的抽象的新世界;一种极端高深而且艰巨水平的抽象。这些哲学家的思想和论证在学生看来有时不仅难于理解,而且好像与它们没有什么关系,因为他们发现不了有什么事情与它们有吴系。然而学生知道这些人都是伟大的哲学家,而哲学就是这个样子讲的。因此他们就努力使自己的思想光适应这种他们认为的(我们将看到是错误地认为的)这些哲学家的思维方式。他们将试图讲这些哲学家的奇怪语言,模仿他们的折磨人的螺旋论证,甚至把自己捆在他们古怪的绳结中。有的可能肤浅地学会这些手法,别的人则可能成为这些手法的真正醉心者。然而有些人经过努力最后达到可能如维特根施坦所描述的结论:“我已经和任何人一样,学会了行话。这是很巧妙而且吸引人的。事实上,它吸引人到危险的地步;因为事情的简单真相是,它只是庸人自扰——只是一派胡言乱语。我觉得我们应当尊重这种人。”
我认为这样一个结论是严重错误的;然而我敢说这几乎是这里所谓的讲授哲学的有效方法不可避免的结果。(当然,我并不否认有些特殊天才的学生可能在大哲学家的著作中发现比这个故事所讲的更多的东西——而且并不自欺。)因为学生发现激起那些伟大哲学家的超哲学问题的机会(数学的、科学的、道德的和政治的问题)确是很小的。一般地说,这些问题只有通过研究科学思想史,特别是当时的数学和科学的问题状况才能发现;而这就要预先肯定研究者对数学和科学相当熟悉才行。只要懂得当时科学中的问题状况,那些研究大哲学家的人才懂得那些哲学家试图解决什么迫切而具体的问题,那些他们认为不能避而不谈的问题。只有在懂得这一点以后,研究者才能发现关于伟大哲学家的一种不同图画——一张使表面看来像是胡说成为可理解的图画。
我将试图借助事例来建立我们的两个论题,但在转到这些事例以前,我要总结一下我的论题,而且把我跟维特根施坦的账讲讲清楚。
我的两个论题总起来说是,哲学深深扎根于哲学之外问题中,维特根施坦的否定判断总的说来,就哲学而言是对的,因为哲学已经忘却了它的哲学以外的根源;这些根源很容易为研究哲学的哲学家忘掉,而不是受非哲学问题的压力被迫钻入哲学。
我对维特根施坦学说的看法可以总结如下。总的说来,不存在纯哲学问题,这或许是真的;因为的确哲学问题变得愈纯粹,就愈会丧夹其原始意义,它的讨论更易于堕落为空洞的文字游戏。另一方面,不仅存在着真正的科学问题,而且也存在着真正的哲学问题。即使经过分析,发现这些问题含有事实成分,也用不着列为属于科学一类,而且即使他们应该用纯逻辑的手段来解决,也不需要列为逻辑的或套了逻辑的问题。物理学中就出现了类似的情形、例为,解释某些光谱名词(借助于关于原子结构的假说)可以最后发现用纯数学演算来解决。但这仍然并不意味着这个问题属于纯数学而不属于物理学。我们完全有理由说,如果与物理学家传统讨论过的问题和理论有关(例为物质构造的问题),即使用来解决它的方法证明是纯数学的,仍将有理由算为‘物理)的问题。正如我们刚才看到的,许多问题的解决可以侵入许多科学的界限。同样,如果我们发现,一个问题虽说原来是由原子论引起的,但这个问题和过去哲学家讨论的问题和理论的关系,比今天物理学家研究的那些理论的关系要深些,那就可以正确地说这是个“哲学”的’问题。而且)这和我们解决这问题时所使用的方法一点没有关系。例如宇宙学常常具有巨大的哲学意义、虽则它在某些方法上也许已经变得和所谓“杨理学”的关系更密切了。说它由于讨论的是事实问题,就必须属于科学,而不属于哲学,这不仅是学究气,而且结果显然是一种认识论的教条,也就是一种哲学教条。同样,用逻辑方法解决的问题也没有理由否认其“哲学的”性质。它可能是典型的哲学性质的,或物理性质的,或生物性质的。在爱因斯坦的狭义相对论里,逻辑分析起了一定的作用;使相对论在哲学上有意义并且引起一大堆,和它有关的哲学问题,部分原因就在这里。
维特根施坦认为所有真正的陈述(因此也是所有真正的问题)可以被分为各自独立的两类:事实的陈述(后天的综合性的),这是经验科学所研究的;逻辑的陈述(先天的分析性的)这是纯形式逻辑或纯数学所研究的;维特根施坦的学术发现就是这个论断的结果。这种简单的二分法,对于泛泛的研究来说,虽极有价值,但对许多探索的目的来说则过于简单了。虽然它的意图特别着眼于排除哲学问题的存在,但对这个目的来说,却相当不够有力;因为即使我们承认这种二分法,我们仍然可以主张事实的或逻辑的或混合的问题,在某种情况下,会成为哲学的问题。
四
现在我转到我的第一个例子:柏拉图和早期希腊的原子论。
我在这里的论题是,柏拉图的中心哲学思想是所谓形式论或理念论,只能在一种哲学以外的形势下才能正确地理解;特别是在希腊科学(主要在物质)的要紧关头;其所以是要紧关头是因为发现二的平方根是无理数。如果我的论题是正确的,柏拉图的学说至今还没有为人完全理解。(当然,能达到“完全”理解是非常成问题的。)但是,一个更重要的后果是,它决不能为根据前节里所述的有效方法训练出来的哲学家所理解——当然,除非他们特别掌握到有关的事实。(他们可能必须接受权威的说法——这意味着抛弃上述的讲授哲学的有效方法。)
看来柏拉图的形式论的起源和内容与毕达哥拉斯万物的本质都是数的学说密切相关。这种关系的细节以及原子主义和毕达哥拉斯思想之间的关系也许不太为人知道。所以我将照我现在对它的了解,将其简单经过叙说一下。
看来,毕达哥拉斯的集团或派别的创始人深深受到两个发现的影响。第一个是表面上纯属于质的现象,如音乐的和谐,实质上以纯数值比率为基础的,1:2;2:3;3:4。第二个值是“直角”或“平角”(例如把一张纸折叠两次,两个折痕交叉而成)与纯数值比率3:4:5或5:12:13(直角三角形的两边)有关。看来,这两个发现导致毕达哥拉斯得出一个异想天开的概括,即万物的本质都是数或数的比例;或者说数就是比例(逻各斯=理性),事物的理性的本质,或者说事物的真正本质。
这个思想虽然奇特,它在许多方面都证明是有收获的。它的最成功的应用之一是简单的几何图形如正方形、直角三角形和等腰三角形,而且还应用于某种简单的立体如棱锥体,这些几何问题的某些研究是甚于所谓磐折形。
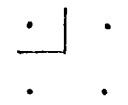
这可以作如下的解释。如果我们用四点表明一个正方形
我们可以把它解释为对上左角的一点增加三点的结果。这三个点是第一磐折形;我们可以这样来表明它:
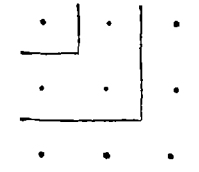
通过加上一个第二磐折形,由更多的五点组成,我们得到
我们立刻看到 ~ 系列奇数的每个数1,3,5,7……,形成了一个正方形的磐折形,而这个总数1,1+3,1+3+5,1+3+5+7,……是正方形数,如果n是(点数在)一个正方形的边,它的面积(点的总数=n2)将等于最先的n奇数的总和。
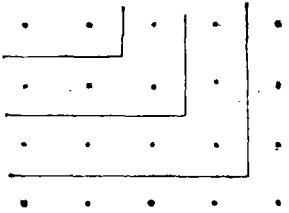
由于正方形的研究,也研究了等边三角形。下面图形可以视为代表一个增长三角形——通过向下增加点的新水平线。
这里每个磐折形是点的一个最后水平线,一系列1,2,3,4,……的每一要素是一个磐折形。“三角数”是总数1+2;1+2+3;1+2+3+4,等等,最先的n自然数的总数。把两个三角形放在一起。
我们还得出长方形的数,那是长方形直角图形的数,其最简单的是
长方形数2+4+6……;一个长方形的磐折形是一个偶数,而长方形数是偶数的总和。
这些研究又被推广到立体;例如把开头的三角形数加起来,就得出棱锥体数。但是它主要应用于平面图形:或形状,或“形式”。这些形式的特征被认为表现在数的适当系列上,也就是说表现在系列的顺序数的比例数上。换言之,“形式”就是数或数的比例。另一方面,不仅事物的形状,而且抽象的性质如和谐和“直”都是数。这样,就得到了数是一切事物的理性本质的理论。
这个观点的发展受到点的图形与星座图形的相似的影响,如狮子座、天蝎座或室女座。如果一个狮子座是一种点的排列,它也一定有一个数。这样,毕达哥拉斯主义似乎与数或“形式”是事物的天体形状的信仰联系起来了。
五
这个早期理论的主要原理之一是基于奇数与偶数之间的基本区别的所谓‘对立表’。它含有这样一些:
人们阅读这个古怪的表,对毕达哥拉斯的思想方式就有点懂了,以及为什么“形式”或几何图形的形状本质上被看作是数,而且一些抽象概念如正义,当然还有和谐与健康,美丽与知识,都看作是数了。这个表所以有意思,还因为它为柏拉图接受了,而且几乎没有什么改变。柏拉图著名的'形式'或‘理念’论,大致说来,的确可以形容为对立表的‘好’的一边构成一个(无形的)宇宙,一个高级实在的宇宙,一个万事万物的不变和固定的形式;一切真的和确定的知识(认识=智能=科学)只能是关于这个不变和真实宇宙的知识,而我们生生死死于其中的变化和流动的眼前世界,这个有生有灭的世界,这个经验的世界,则仅仅是那个真实世界的反映或摹本。这只是一个表象的世界,在这个世界里,是不能获得真实的和确定的知识的。在这里一切能获得的所谓知识只是容易犯错误的凡人的似乎有理的不确定见解和偏见。柏拉图对对立表的理解是受到巴门尼德的影响的,而巴门尼德的挑战则导致了德谟克利特的原子论的发展。
(Conjecture and Reputtation,第2章)
(待续)