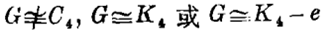哈密顿道路图

发布时间：86年07月25日

Gary Chartrand 编译杨炳儒

[摘要]图G的哈密顿道路图H(G)是和G具有相同顶点集的图，并且其中任意两个顶点u和v是邻接的当且仅当G含有一条哈密顿u-v道路。本文呈现出哈密顿图同构于哈密顿道路图的特征。

1.引言

图G中的道路（圈）称为G的哈密顿道路（圈），如果它含有G的每一个顶点。图是可溯的（哈密顿），如果它含有一条哈密顿道路（圈）。图G是哈密顿——连通的，如果对于G中每一对相异的点u、v、G都含有一条哈密顿道路。

图G的哈密顿道路图H(G)是和G具有相同顶点集的图，并且其中任意两个顶点U和V是邻接的当且仅当含有一条哈密顿u-v道路。于是，图恰好说明哪一些点偶是通过的哈密顿道路而连通的。对于P阶图G，H(G)≌K_P当且仅当G不是可溯的，而H(G)≌K_P当且仅当G是哈密顿 - 连通的。

假设G是一个P（≥2）阶图，并且设n是一个这样的整数：1≤n≤P-1。Escalante，Montejano和Rojano[2]同样地定义了G的n - 道路图G_n，那图和G具有相同的顶点集，并且其中点u到v是邻接的，当且仅当G含有一条长度为n的u-v道路。于是G的(P-1) - 道路图G_P-1是与H(G)同义的。

2.自哈密顿道路图

图G是自哈密顿道路图，如果G≌H(G)。这篇论文是以确定哪些图是自哈密顿道路图的问题为研究对象的。存在着一个等价于这个问题的公式。

哈密顿道路图序列是一个符号序列：

G，H(G)，H²(G)，H³(G)，…，

这里G是一个图，H¹(G)=H(G)，并且对于n≥2，Hⁿ(G)=H(H^n-1(G))。图F表示哈密顿道路图序列的极限，如果存在一个图G并且存在一个正整数n，使得对于每一个正整数K，当K≥n时，都有F≌H^K(G)。

命题图G是自哈密顿道路图，当且仅当G是哈密顿道路图序列的极限。

证明假设G是自哈密顿道路图，则G≌H(G)。因此序列G，H(G)，H²(G)，……的各个元素同构于G，并且G是哈密顿道路图序列的极限。

反之，假设F是哈密顿道路图序列的极限。这就存在一个图G并且存在一个正整数n，使得若K是一个正整数且K≥n时，则F≌H^K(G)。所以，F≌H^K+1(G)= H(H^K(G))=H(F)，并且F是自哈密顿道路图。

我们现在考察一些自哈密顿道路图的实例。首先，观察对于任何的P，K_P和K_P是自哈密顿道路图，并且对于P≥3，H(C_P)≌C_P。

对于n≥2，正则完全偶图K(n，n)是自哈密顿道路图。为了看清这一点，设V₁和V₂是K(n，n)的划分的集合。因为通过哈密顿道路，V₁的任意一点与V₂的任意一点连通，在H(K(n，n))中，V₁的任意一点与V₂的任意一点邻接。在其他方面，V_i（i=1，2）中没有两个相异的点是通过K(n，n)中的哈密顿道路连通的。所以，在H(K(n，n))中没有两个V_i（i=1，2）中的点是邻接的。于是，H(K(n，n))≌K(n，n)。按照同样的方式，当n≥2时，图K_n+K_n（K_n和K_n的并）是一个自哈密顿道路图。

圈C的弦是一条联结C中两个非相邻顶点的边。P（P≥4且为偶数）阶的图G称为弦加法的，如果G的顶点可以标记成这样：（1）v₁，v₂，…，v_P，v₁是G中的一个哈密顿圈C；（2）对于每一个偶整数i（2≤i≤P），deg_Gv_i=2；（3）C含有弦；（4）v_jv_K是C中的弦，对于任意整数l意味着v_j+2lv_K+2l是C中的弦，这里下标是以P为模的（在通常称作循环的图中，弦加法的图的结果对于度为2的点不成立）。弦加法的图必然有唯一哈密顿圈，即C。插图1是弦加法的。

作为引言中的主要推论，弦加法的图展现在下列结果中。

引理1 每个弦加法的图都是自哈密顿道路图。

证明设G是一个P（P≥4且为偶数）阶的弦加法的图，于是G的点可标记作v₁，v₂，…，v_P，这样，弦加法的图的定义中的条件（1）-（4）是满足的。

通过Φ(v_i)=v_i+1定义Φ：V(G)→V(H(G))，这里下标是以p为模的。我们说明Φ是一个从G到H(G)的同构。设v_j和v_K是G的邻接顶点，我们验证Φ(v_i)和Φ(v_K)在H(G)中邻接。

首先，假设K=j+1，即v_j和v_K在G的哈密顿圈C中是相邻的。那么，显然G含有一条G中的哈密顿v_j+1——v_j+2道路，所以v_j+1和v_j+2在H(G)中是邻接的。另外，假设v_jv_K是一条C的弦，这里的j和K是奇数。那么G含有哈密顿道路。

v_j+1，v_j+2，…，v_K，v_j，v_j-1，v_j-2，…，v_K+1

并且v_j+1v_K+1是H(G)中的一条边。

其次，我们说明那H(G)不含有其他边，因此完成了引理的证明。要想证明它，我们考察G中可能的哈密顿道路，并且设2度点（具有偶下标的）在本文中称为偶点，而那具有奇下标的称为奇点。图G有相同数量的偶点和奇点，并且没有两个偶点是邻接的。于是没有始点和终点都是奇点的哈密顿道路。同样，若G中的哈密顿道路其始点是一个偶（奇）点，而终点是一个奇（偶）点，则偶点和奇点必须是交错的，所以这条哈密顿道路是C的子道路。

存在着剩下的可能是G有一条哈密顿道路，其始点和终点均为偶点。设P是一条G中的哈密顿v_j+1——v_K+1道路，这里的j和K是奇数并且v_jv_K?E(G)。那么P恰好含有一个子道路v_a，v_b，这里a和b均为奇数，所以v_av_b是C的一条弦。因为P的所有其他边是属于C的，道路P可以表示为

v_b+1，v_b+2，…，v_a，v_b，v_b-1，…，v_a+1

或为

v_b-1，v_b-2，…，v_a，v_b，v_b+1，…，v_a-1

这里下标是以P为模的。在第一种场合，a=K和b=j，这样的v_jv_K∈E(G)；假设相反，在第二种场合，a=K+2和b=j+2，这样的v_j+2v_K+2∈E(G)。因为G是弦加法的，这意味着v_jv_K∈E(G)，矛盾。

我们猜想自哈密顿道路图的实例，在事实上有我们提出的那些实例。

猜想 P阶的图G是自哈密顿道路图，当且仅当G是弦加法的或者G是同构于图K_P，K_P，C_P（P≥3），K(?P，?P)和K_P/2+K_P/2中的某一个，最后两个中的P为偶数。

3.哈密顿、自哈密顿道路图

在这一节中，我们给出两个重要的结果，即在哈密顿图的情况下，对上述猜想的验证。开始我们有初步的结果。

跟G的哈密顿圈C—起考虑的是在其旁的G的外圈，它是G的恰好含有C的一个弦的、中间的一个圈。

引理2 设G是一个P(≥4)阶的哈密顿、自哈密顿道路图，它具有哈密顿圈C：v₁，v₂，…，v_P，v₁和弦v₁v_m，v₂v_m+1，这里2＜m＜P。那么

（ⅰ）C含有所有形如v₁v_m+i-1的弦，这里i=1，2，…，P，并且这里所有的下标是以P为模的；

（ⅱ）若m≥5，G含有一个长度为m-2的外圈。

证明对于i=1，2，…，P，图G含有一条哈密顿v_i-v_i-1道路，这里v_P+1=v₁。因此，H(G)含有边v_iv_i+1，于是含有哈密顿圈C。

因为v₁v_m是C的弦，图G含有哈密顿v₂-v_m+1道路

v₂，v₃，…，v_m，v₁，v_P，v_P-1，…，v_m+1。

类似地，G含有一条哈密顿v_P-v_m-1道路。因为v₂v_m+1是一条C的弦，可见G含有一条哈密顿v₁-v_m道路和一条哈密顿v₃-v_m+2道路。因此，H(G)含有边v_Pv_m-1，v₁v_m，v₂v_m+1和v₃v_m+2。按照同样的方式，我们看到H²(G)有哈密顿圈C和弦v_P-1v_m-2，v_Pv_m-1，v₁v_m，v₂v_m+1，v₃v_m+2和v₄v_m+3。按照这种方式继续下去并且应用那个事实：G≌H(G)≌H²(G)≌…，我们注意到G含有所有的弦v_iv_m+i-1，这里i=1，2,…，P并且所有下标均以P为模。这就证明了（ⅰ）。

若m≥5，则v₁，v_m，v_m+1，v_m+2，…，v_P-(m-3)，v₂，v₃，…，v_m-1，v_P，v_P-1，…，v_P-(m-4)是G中的一条哈密顿v₁-v_P-(m-4)道路。这意味着v₁v_P-(m-4)是H(G)并且是如此地H(G)中的一条弦，因而G有一条长度为m-2的外圈，因此证明了（ⅱ）。

定理设G是一个P(≥3)阶的哈密顿图。那么G是一个自哈密顿道路图当且仅当G是弦加法的或者G同构于K_P，C_P，K(?P，?P)和K_P/2+K_P/2，最后两个中的P为偶数。

证明我们已经说明了图K_P，C_P，K(?P，?P)和K_P/2+K_P/2中的每一个都是自哈密顿道路图。由引理1，每个弦加法的图是自哈密顿道路图。因此，足够去证实它的逆。

设G是一个P(≥3)阶的哈密顿、自哈密顿道路图，若G≌C_P，证明是完成的；于是我们假定G是设有圈的。

在G的哈密顿圈之中，设C：v₁，v₂，…，v_P，v₁是使G包含一个最小长度为m的外圈的一个，即圈v₁，v₂，…，v_m，v₁。注意3≤m≤?(P+2)。若v₁v_K是C的一个弦，则通过使用在引理2（ⅰ），中所使用过的同样论据，我们看到所有的图G，H(G)，H²(G)等等，含有哈密顿圈C；H(G)含有弦v_Pv_K-1和v₂v_K+1；H²(G)含有弦v_P-1v_K-2，v₁v_K和v₃v_K+2等等。特别是，这意味着G含有弦v₁v_K；H²(G)含有v₁v_K和v₃v_K+2；H⁴(G)含有v₁v_K，v₃v_K+2和v₅v_K+4等等。

现在我们按照同等的P，考察两种情形。

情形1 假设P是奇数，在这情形中我们说明G≌K_P。

从上文提到的情形观察，H^P+1(G)含有弦v₁v_m，v₃v_m+2，…，v_Pv_m-1和v₂v_m+1。因为H^P+1(G)含有弦v₁v_m和v₂v_m+1，并且G≈H^P+1(G)，我们由引理2断定：（ⅰ）G含有所有形如v_iv_m+i-1的弦，这里i=1，2，…，P且所有下标均以P为模；（ⅱ）m=3或m=4。

假设m=4，且记奇整数P=3K+r，这里K≥2且r=0，1或2。在下列的每种情形中，均表明道路是哈密顿v₁-v_P-1道路，意指H(G)含有一个外三角形，产生矛盾，故m=3：

r=0：v₁，v₄，v₇，…，v_P-2，v_P-3，v_P-4，v_P-7，v_P-6，v_P-9，v_P-10，…，v₅，v₂，v₃，v_P，v_P-1；

r=1：v₁，v₄，v₇，…，v_P-3，v_P-2，v_P-5，v_P-4，v_P-7，v_P-8，v_P-11，…，v₅，v₂，v₃，v_P，v_P-1；

r=2：v₁，v₄，v₇，…，v_P-4，v_P-3，v_P-2，v_P-5，v_P-6，v_P-9，v_P-8，…，v₅，v₂，v₃，v_P，v_P-1。

因为m=3，G含有所有的弦v₁v₃，v₂v₄，v₃v₅，…，v_P-2v_P，v_P-1v₁和v_Pv₂。所以，G含有像圈C的平方一样的子图。（图F的平方F²是有着与F—样的点集，并且在其中两个点是邻接的当且仅当在F中这两点间的距离是1或2）。因为2—连通图的平方是哈密顿 - 连通的（见[1]），G是哈密顿 - 连通的，所以H(G)≌K_P，于是G≌K_P。

情形2 假设P是偶数。这情形又可分为两个子情形。

子情形2a。假定G含有长度为偶数的外圈。设n是G的小的偶外圈的长度。不失一般性，我们可以假定v₁v_n是一条G的弦，这里4≤n≤1/2(P+2)。

假设n=4。那么G含有弦v₁v₄，v₃v₆，v₅v₈，…，v_P-3v_P和v_P-1v₂。于是，若v_a，v_b∈V(G)，这里a是奇数而b是偶数，则对于b=a-1，a+1或a+3，v_av_b∈E(G)。设a和b各自是奇的和偶的整数，这里1≤a＜P，1＜b≤P，并且b对于a-1，a+1和a+3是不同的。我们说明这里也是v_av_b∈E(G)。下列就是G中的一条哈密顿v_a-v_b道路：

v_a，v_a+1，v_a+2，…，v_b-1，v_b+2，v_b+3，v_b+6，v_b+7，v_b+10，…，v_a-6，v_a-3，v_a-2，v_a-1，v_a-4，v_a-5，v_a-8，v_a-9，…,v_b+1，v_b。

所以，v_av_b是H(G)的一条边，意指H(G)且因而G含有与K(?P，?P)—样的子图，有划分的集合V₁=｛v_i|i是奇数｝和V₂=｛v_i|i是偶数｝。

若G不含有长度为奇数的外圈，则G≌K(?P，?P)。另外，在V₁中或在V₂中都存在着点与点的邻接，这在前面已说到。那么，若v_x和v_y是V₂中相异的点，在那里存在着G中的一条哈密顿v_x-v_y道路，它们就意味着H(G)，并且因此也意味着G，含有像并K_P/2+K_P/2一样的子图。若G不含有其他边，则G= K_P/2+K_P/2；另外G≌K_p。

现在假定n≥6。我们说明这是不可能存在的情况。因为P是偶数，对于一些i，1≤i≤?(n-2)，P=2i[mod(n-2)]。因此我们可以记作P=K(n-2)+2i，这里K≥2，因为P≥2n-2。

回想到G含有所有的弦v₁v_n，v₂v_n+2，v₅v_n+4，…，v_P-n+1v_P和v_P-n+3v₂…，v_P-1v_n-2。我们以v₁为始点的道路列下：

v₁，v_n，v_n-1，v_2n-2，v_2n-3，v_2n-4，v_3n-5，v_4n-6，…，或等价的。

v₁，v_(n-2)+2，v_(n-2)+1，v_2(n-2)+2，v_2(n-2)+1，v_3(n-2)+2，v_3(n-2)+1，v_4(n-2)+2，…（1）

我们用这种方式延伸这条道路，直到v₂，v₃，…，v_n-2的某一个顶点。或者，更确切地到点v₂，v₄，v₆，…，v_n-2的某一个。这个点实际是对于j_i＞P时序列（1）中的第一个点v_ji。事实上，

j_i=(K+1)(n-2)+2=K(n-2)+n=K(n-2)+2i+(n-2i)，

即v_ji是v_n-2i，就是点v₂，v₄，v₆，…，v_n-2中的某一个。

若v_ji≠v₂，我们用相同的方式延伸（1），获得

v₁，v_(n-2)+2，v_(n-2)+1，…，v_j₁，v_j₁_-1，v_j₁_+(n-2)+2，v_j₁_+(n-2)+1，v_j₁_+2(n-2)+2，…（2）

最后重新得到点v₂，v₄，v₆，…，v_n-2中的某一个。这将是v_n-4i或v_(n-4i)+(n-2)两者之一，随i的值而定之。称这点为v_j₂。注意，无论j₂取怎样的值，我们都有j₂≡n-4i[mod(n-2)]。

若v_j₂≠v₂，我们像上文一样延伸。这过程和序列（2）是延伸到v₂为止的。对于假设d=gcd(i，?(n-2))这必定会出现。于是因为n-[(n-2)/2d]2i≡2[mod(n-2)]，结果产生v_j(n-2)/2d=v₂。

若v₁-v₂道路P₁恰好是哈密顿道路（意指d=1的那个），则G有一个哈密顿圈含有边v₁v_n，所以H(G)含有边v₁v_n。因为H(G)也含有边v₂v_n+1，我们可以应用引理2，和n≥6的假定矛盾。

若P₁不是哈密顿的（因而d≥2），则因为j_a-j_b是关于1≤a＜b≤(n-2)/2d中2d的倍数，导致2d+2是使得v_2d+2属于P₁的大于2的最小正整数。特定地v₄（且因而v₃）是不属于P₁的。我们以道路P₂的v₃作始点，恰好进行到P₁像具有终点v₄—样为止。这过程延伸到最后产生道路P_d为止。那么，P₁，P₂，…，P_d是一条G中的哈密顿v₁-v_2d道路，这意味着H(G），因而也意味着G，含有一条长度为2d的外圈。因为2d≤n-2，这便引出矛盾。