这是一个奇怪的事实:搞密码通讯的政府部门反由于数学家的无知而获益。
“原子论”——相信原子是“不可分割的东西”——主导着古希腊的学术研究。原子论者认为不仅万物由原子构成,数也是如此。欧几里德和他的同代人认识到某些整数,例如2,3,5,7和11本质上是不可分的。仅能被自己和1整除的数称作素数。另一些数如4,6,8,9,10等就不是素数,因为它们还有其他因子。我们说这些数是合成的,因为它们都唯一的由一些素数相乘而“合成”。例如4=2×2,6=2×3,8=2×2×2,9=3×3和10=2×5。
一个大得惊人的素数
今天,已知的最大素数是一个有39761数位的庞然大物,它等于2的132049次乘方减1。要把这个数的每个数字写出来需要本刊的五个版面①。去寻找比已知最大素数更大的素数,并探讨其性质一向是我们这个最古老的数学分支——数论(或整数的研究)的一个课题。
数论仅是貌似简单的。它的主要定理经常可以被叙述得使每个人都能理解,但其证明——当它们被知道的时候——可能需要高深复杂的数学。例如在1742年,普鲁士出生的数学家哥德巴赫(Christian Goldbach)提出一个猜想说每个大于2的偶数是两个素数的和。据此,4=2+2,6=3+3,8.3+5,10=5+5等等。借助于计算机,数论学家已经把直到一亿的所有偶数拆开为两个素数的和,但他们还不能证明哥德巴赫的这个简单猜想普遍地成立。人们对它的尝试可不少,在以往的两个半世纪中,最有才能的数学家们曾经专心研究过它。
在所有的数学分支中,数论在传统上最远离自然世界。属于其他高深的数学领域的一些似乎很抽象的结果已在物理学,化学和经济学方面派上好用场了。然而数论的许多结果还未有应用。如果哥德巴赫猜想一旦被证明了,数学家们将会欢欣鼓舞,但是物理学家和化学家们也不知道如何应用这个结果,即使它真有什么应用的话。因此,对于素数的研究一直被看作是最纯粹的,未被应用沾染的数学。在几个世纪以前,这种纯洁性使数论赢得了“数学的皇后”的美名。
然而,今天这位皇后的尊严却受到损害。素数,这些一尘不染的臣民,竟屈尊俯就子国家安全名下的低下工作了。据说我们政府所用的一些最机密的密码就是依赖素数的。这些将字母转换成数字的密码的基础是一种严整的数学理论:某些计算程序是比较容易执行的,但其还原过程却难得惊人。例如用计算机算出两个100位的素数的乘积是极容易的事,但是反过来要从这个有200数位的乘积找到它的两个100位的素数因子却极其困难(除非有人告诉你)。这一点意味着要破译这一种密码是很费人心机的。能够将文电编码的人无须会译码,他仅须知道这个有200数位的乘积就够了。但是文电译解人还必须知道这两个素数因子,仅知道它们的乘积是不够的。
这一类密码被称为明码的密码术,因为它可以高度公开的方式被使用。如果我要别人给我发送秘密文电,我只要公开这个二百位的数(并说明如何用它编码),则我所要求的任何对象都能给我发送密码文电,我对这两个素数因子严守秘密,我就是唯一能译解这种密电的人。然而,这种密码之所以成功,唯一的理由是数论学家至今仍然未能解决如何把巨大的合数分解为素数因子的问题。
—位著名的素数学家、佐治亚大学的波梅兰斯(Carl Pomerance)说:“这种密码系统是由于适逢无知而成功的一项应用。由于这种密码,有更多的人研究数论了。面对分解因子问题伤透脑筋而又束手无策的数学家越多,这种密码就越好。”这种密码系统的成功还在另一方面依赖数论:必须用复杂的数论方法鉴别出作相乘之用的100位以上的素数。
由于素数被用在最先进的密码上,我要列举关于它们的一些已知结果和未知结果。大约在二千三百年前,欧几里德已证明素数是多至无尽的,他的证明仍然是数学上简明和优美的典范。
欧几里德的优美证明
欧几里德论述:假定只有有限多个素数。则其中必有一个最大的,称作P。现在考虑一个大于P的数Q,它等于1加上从1至P的相继整数的乘积,即Q=1+1×2×3×…×P。从Q的形式可以看出从2到P的所有整数都不能把它除尽;每次相除都留下一个余数1。如果Q不是素数,则它能被某个大于P的素数整除。另一方面,如果Q是素数,Q本身就是一个大于P的素数。不管哪一种可能性都意味着存在一个比最大素数更大的素数。这当然意味着关于最大素数的构想纯属虚幻。但是如果没有这样一个最大素数,则素数的个数必须是无限的。
数学家们长期梦想着能找到一个公式,当式中的n取从0至无限大的整数时将给出所有的素数。欧拉(Leonhard Euler),这位十八世纪的数学奇才,反复玩赏一个使人神往的简单公式n2+n+41。当n=0,这个公式产生素数41。当n=1,产生素数43。当n=2,产生素数47。的确,当n取从0至39的相继整数时,由欧拉的公式产生的无一不是素数。但当n=40时,公式突然失效,结果是1681,是41的平方。
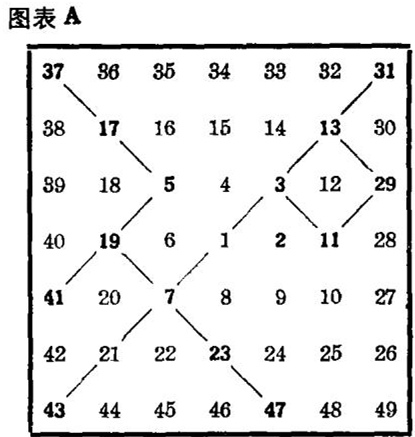
1983年,乌拉姆(Stanislaw Ulam),这位曾在洛斯阿拉莫斯对原子弹做过先驱研究工作的卓越数学家,在一张纸片上无意地乱写数字时,草草写出一些相继的整数,从1开始沿方螺旋线由里向外环绕(图表A)。使他惊奇的是,他漫不经心中写出的素数(图表中用粗体字表示)倾向于落在斜线上。受到这个偶然的幸运的发现的鼓舞,乌拉姆和他的两个合作者威尔斯(Mark Wells)和斯坦因(Myron Stein)研究了一些从异于1的整数开始沿方螺旋线排列的数字方阵。图表B表示从41 ~ 440的整数的这种螺旋线。再一次显示出,素数经常落在斜线上。从421 ~ 383的主对角线对应于由欧拉的简单公式n2+n+41产生的素数。
1963年,在洛斯阿拉莫斯的高速电子数字计算机二号(Maniac Ⅱ)主机的存储器里存储了最前面的九千万个素数。威尔斯回忆说:“在洛斯阿拉莫斯,我们具备了一项第一流的绘图设备,用计算机描出了素数,这使我们非常兴奋。”、Maniac Ⅱ画出一个显示出所有小于一千万的素数的方螺旋线图表。确实,多数素数非常神奇地沿斜线聚集。
欧拉的公式n2+n+41结果对于大数值的n是非常好。Maniac Ⅱ计算出,由这个公式产生的小于一千万的数中,有47.5%是素数。它对于较小的n更为成功。当n在2398以下时,这个公式产生素数和非素数的机会各占一半。对于从1至100的n,它产生86个素数,仅产生14个合数。
乌拉姆和他的合作者还发现了其他一些几乎和欧拉的公式一样好的产生素数的公式。由公式4n2+170+n+1847产生的小于十万的数中,有46.6%是素数,其中有760个素数是不能由欧拉的公式产生的。公式4n2+4n+59,产生素数的成功率是43.7%,并产生1500个不能由前述的两个公式产生的素数。
最大的矛盾是,尽管有这么高的产生素数的成功率,尽管在方阵螺旋线中素数有显然的斜线分布的规律,数论学家已经证明并无一个与欧拉的公式相类似的公式能产生所有的素数②。但这个结论并未能制止寻求素数分布规律的痴心狂想。
在最初的100个数中,有25个素数:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89和97。在这些素数和随后的其他无穷多个素数之间的间隔并无明显的模式可循。因为2是仅有的偶素数,所以2和3是仅有的相差为1的一对素数。
相差为2的素数对——称为孪生素数——又怎么样呢?在最初的25个素数中,有8对孪生素数:(3,5),(5,7),(11,13),(17,19),(29,31),(41,43),(59,61)和(71,73)。几乎150年以来,数论学家们一直猜测,孪生素数对也像素数那样是多至无穷的,但至今还得不到证明。重大的进展是中国数学家陈景润于1966年作出的,他证明了存在无穷多个相差为2的如下数对,其中第一个是素数,第二个是素数或两个素数的乘积。(一个合数如果仅是两个素数的乘积,称为“准素数”,这个用语表现出数学家们的迫不及待的乐观心理,以及真正的素数是多么难以掌握。)
还有另一件乐观的事,陈景润证明了哥德巴赫猜想的一个较弱的情形:每个“充分大”的偶数是一个素数与一个准素数的和。“充分大”是数论文献中的一种委婉的说法,意思是“我知道我的证明对于大于某一个Q的所有整数是成立的,但我不知道Q是什么数”。尽管有术语“充分大”的含糊性,数学家们仍然认为陈景润的证明是数论在以往三十年中最重大的成就。
关于素数之间如何远离方面的已知知识比在如何密集方面的更多。其实,很容易证明存在任意长的非素数的相继整数的序列。设n!表示从1至n的相继整数的乘积。从它的构成可知,它能被从2到n的所有整数整除。现在构造如下相继整数的序列:n!+2,n!+3,n!+4等直至n!+n。这个序列的第一项n!+2能被2整数;第二项n!+3能被3整除;第三项n!+4能被4整除,等等。这是一个有n-1个数的序列,其中没有一个素数。只要选取任意大的n,你可以得到任意长的没有素数的相继整数的序列。
然而,多素数的序列也很多。事实上,数论学家们相信素数能形成任意长的算术级数。容易找到短的算术级数,例如素数3,5,7形成一个三项的公差为2的算术级数(1944年,证明了有无穷多组三素数能组成算术级数,但在每组中,素数不一定是相继的)。素数199,409,619,829,1039,1249,1459,1669,1879和2089构成一个10项的算术级数,公差为210。级数越长,首项素数和公差急剧陡增,要发现它们很困难。1984年,康奈尔太学的普里切尔德(Paul Pritchard)还是发现了有19个素数组成算术级数;首项素数是8297644387,公差是4180566390。
有些数学家还猜想,存在任意长的相继素数的算术级数。例如相继的素数1741,1747,1753和1759形成一个四项的公差为六的算术级数。然而,关于素数算术级数的这个猜想,即使其中的素数无须是相继的情形至今还得不到证明。
关于素数的已知结果和未知结果,大有文章可写。举一个更简单的例子就够了。已经证明在任意数加一和这个数的二倍之间必有一个素数(这个证明的一个奇妙的推论是至少有三个素数具有任意给定的位数)。但至今还无人证明在任意数的平方加一到这个数加一的平方之间是否一定有一个素数。
因为素数本身的分布并无已知的规律可循,也许唯一合适的说法是,对于数学家们已能证明的关乎它们的东西本来就没有明显的奥妙和理由可寻。某些基本定理——有无穷多个素数,两个相继的素数可以相差任意大一有了最简单不过的证明。其他定理,例如哥德巴赫猜想,有不赞成的证明,虽然没有一个自信的数学家怀疑他们的真理。要取得进展,数论学家权且就准素数和“充分大的数”来证明这些定理。这个领域所需要的是另一个欧几里德或欧拉。至今,我们仍然停留在一种奇怪的处境里:政府和工业界那些依赖秘密通信的部门还继续由于数学家的无知而获益。
[Science Digest,1985年10月]
译者附记 用素数编码简介
这种编码是用计算机完成的。选择充分大的r,并选择两个至少有2r+1数位的素数P1和P2,求出它们的乘积q。选择S与Φ(q)=(P1-1)(P2-1)互素(Φ(m)表示小于m并与m互素的自然数的个数,如果P是素数,则Φ(P)=P-1,如果P1,P2均为素数,则Φ(P1P2)=(P1-1)(P2-1)。
在编码时:将文电加以划分,使每一段有r个字母,作为一个“词”。将文电的每个字母转换成二位数组,26个字母分别对应于数组01,02,03,…,26,空格对应于00。所以每一个词被转换成一个2r位的数。设W是这样的一个2r位的数,作W的S次乘方,并求出关于模q的剩余。即求得WS≡Z(modq),Z<q, Z就是用于发送的W的代码。
如果文电接受人知道Φ(q),她能从方程St≡1(modΦ(q)解出t(由于S与Φ(q)互素,一定能解出t)。要译解这个密码只要将所收到的数字代码Z作t次乘方,求出关于模q的剩余W',它必定等于原来的数字文电。由于当W与q互素时有WΦ(q)≡1(modq),所以W'≡Zt≡(WS)t≡W(modq)。因为W和W'都小于q,它们必定相等。
要选择P1,P2是不少于2r+1位的,是为了保证P1,P2和q将大于每一个词,从而与每个词互素。
这种密码为什么这么有效呢?
如果敌方想破译这一种文电。甚至假定他还知道这个文电所用的q和S。他所要做的就是分解q,求出Φ(q),并求解St≡1(modΦ(q))。但当r足够大时第一项任务就是一个无法解决的问题,这正是这种密码保密的关键。
设r=50,q是两个101位的素数P1和P2的乘积。在当时,如果不知道这两个素数因子要分解即使用最快的计算机也要几十万亿年的时间。(另一方面,如果q的因子是已知的,用计算机求出t,并译解此密码不过是几秒钟的事)。因此,除非q的因子被泄露,这种密码是不可能被破译的。
可是,近几年在因子分解方面已有突破,有可能用一天的时间分解一个85位以上的数,现在这种密码系统的安全性将要成问题了。
———————
① 译者注——现在,新发现的最大素数是2的216091次乘方减1,它有65050数位,写出来要占8个版面。
② 译者注——关于能产生素数的其他形式的函数,有下述定理:函数
F(x,y)=(y-1)/2[∣B2-1∣-(B2-1)]+2,
B=x(y+1)-(y!+1)
当x和y都是自然数时,只产生素数值,给出所有的素数值,并且每个奇数值正好各取一次。(见《数学译林》1984年第3期)