自然、界中许多图形看起来似乎没有什么规律。如连绵的山峰、天空的浮云、曲折的海岸线、蜿蜒的河流、地面或玻璃等固体上的裂纹或断面、水中冉冉漂动的浮游物等等,各式各样,举不胜举。但在这些初看起来无规可循的图形中是否具有某种整体上的统计性规律呢?计算机的飞跃发展以及随之而来的图像处理技术的进步,使这个问题具有强烈的吸引力。如下所述,许多复杂的图形中都隐含着一种简单的规律,即“自相似性”。这类图形多得出人意料。曼德尔勃罗特(B. B. Mandelbrot)致力于这方面的研究,并给出了对这类图形进行分类的线索——“分形”(fractals)。
1. 分形与分维
当我们用地图来观察复杂的海岸线时,比例尺越大,所描绘出的凸凹部分就越详细,但海岸线本身形状的复杂性并没有多大变化。即是说,海岸线的长度是无法准确定义的,它要依赖于地图所采用的比例尺。在许多复杂图形中取出一部分来放大到原来的大小,看起来仍然与原来的图形没有什么区别,这就是所谓“自相似性”(self-similarity)。不论是像有名的寇赫(Koch)曲线那样几何性的图形还是像海岸线那样统计性的图形,所有具有这种自相似性的复杂的图形,统称为“分形”。这类图形的特征在于除了本身的大小以外,不存在能表示其内部构造的特征尺度。
那么,怎样才能定量地描述这种自相似性呢?在上述海岸线问题中,只要能弄清两地点间沿海岸的距离是怎样随比例尺的放大而增加的,就可以表现其特征了。实际上,曼德尔勃罗特正是以这种想法为线索,作为自相似性的定量化指标而引入“分维”(fractal dimension )(又叫“分数维”)这一概念的,它成为通常整数维概念的自然推广。
关于自相似图形分维的求法,有多种等价的方法,可以根据不同的问题选择简便的途径。曼德尔勃罗特在他1982年的《自然界中的分形几何学》(The Fractal Geometry of Natwre)—书中对此作了详细说明。近几年,在日本也有不少文献介绍了分维的求法。初次接触分形概念的读者,最好根据有关文献所介绍的方法亲自试求一下自己感兴趣的海岸线或河流等的分维。
现已测算出大多数海岸线是分形、金属断面也是分形。更有趣的是,有人还研究了云在地面投影的二维图形的边界,发现在云面积为1 ~ 108平方公里范围内,这种曲线是分形,其分维数为大约1.35。表面看来纷乱无序的云竟然也在如此宽广的范围内存在着同一规则!
2. 对随机生长图形的研究
自相似图形实在多得诱人,求出它们的分维数并对图形加以分类等等也不乏趣题。而更有魅力的问题是,探讨这些图形为什么会成为自相似的,它们为什么会具有特定的分维。但自然界中图形的生成机制往往不是单一的,经常有多种因素交织在一起。这种情况下,我们可以假设一种只考虑其最本质的物理机理的理想化模型,对由此生成的图形的性质进行研究。虽然目前对大多数模型还没能给出明确的解析结果,但只要利用近年飞速发展的高速度大容量计算机进行摹拟,也可以相当详细地了解图形的统计性质。对图形的自相似性的检验以及分维的确定都不难做到;通过详细地考察图形的生长过程还可以在一定程度上推断分形结构本身的成因;如果再进一步能通过实验,证实在相应的近于理想化的条件下所生成的实际图形的性质与计算机摹拟结果一致的话,那就可以认为已经基本上弄清了这种图形。
自然界中很多无规图形都是在运动过程中生成的。如雷电、破损、凝集等就是这类运动过程。最近,从不同领域提出了许多种有关图形生长过程的概率性模型,这些模型都将其生长过程作了某种理想化的假设。它们的统计性质已经引起了人们的重视。以下就列举一些代表性的模型。为了叙述简单,只要不再声明,均指在二维正方格子上进行的图形生长摹拟。
1)艾登(Eden)模型:这是一种癌细胞增殖模型。在从原点开始生长的图形的边界外围所有相邻点(方格)中,等概率地任意选一点,使之成为原图形的一点,这样不可逆地进行下去,使图形不断生长。
2)扩散场中的凝集模型(diffusion-limited aggregation),简称DLA:是以布朗运动粒子不可逆地附着到一个核上,使图形不断长大。下节将进一步说明。
3)Rikvold(雷克沃尔特)结晶模型:用有限范围的屏蔽作用来代替扩散场,并对表面张力的作用也作了概率性的考虑。
4)放电模型(Sawada-Ohta-Yamazaki-Honjo模型),简称SOYH:是一种放电对介质破坏的模型。提出放电图形分枝的尖端从侧面向外延伸R倍的概率较大。
5)渗流模型:这是研究在含有某种液体(如石油)的多孔物质内注入另一种不相溶液体(如水)而产生的渗流情况的模型。首先将全部格子点分别设为(0,1)中的随机数,然后,在从原点开始生长的图形(代表水)的所有相邻点中,选择随机数最小的点,设它对于渗流的阻力最小,便将这一格加入到图形中去(就像水推挤石油向前渗流一样),使图形不断生长。
6)加成聚合模型:这是一种高分子支化聚合反应或溶胶凝胶转变过程的模型。放置在各格子点上的具有两个以上结合键的单体在以适当浓度分散着的反应活性剂的作用下开始反应,生成聚合物。
7)逐组凝集模型(kinetic cluster aggregation),简称KCA:这是一种分散胶体的不可逆凝集模型。后节将进一步说明。
上述各种模型的规则特征,可以归纳为两点。其一,是在图形界面上局部生长的规则。例如Eden模型中从边界相邻的任一点生长;或者DLA模型中从布朗粒子所到达的边界相邻点生长等等。其二,是图形处于某种“场”中。例如DLA模型中,粒子在附着到图形上之前是在作布朗运动,这就相当于作了一个扩散场,而图形则处于这种“场”中。
同时兼有以上两个特征的模型只有DLA和KCA,其他各种模型都只具有第一个特征。
这些生长模型与实际现象联系密切,都有很深的意义。其中特别是与凝集现象有关的DLA和KCA还值得进一步加以说明,其理由是:a)凝集过程本身就是在大部分科学领域中都能见到的最普遍的现象之一;b)两个模型都将凝集过程极端地简化了,因而,应用范围很广,其适用性可能超出凝集现象的范围;c)在大型计算机使用容许范围内,两种模型生成的图形始终是自相似的,其分维数都只取决于空间维数;d)它们具有在非平衡状态下所生成图形的特有性质等漂亮的统计物理学特征。
3. 关于DLA模型
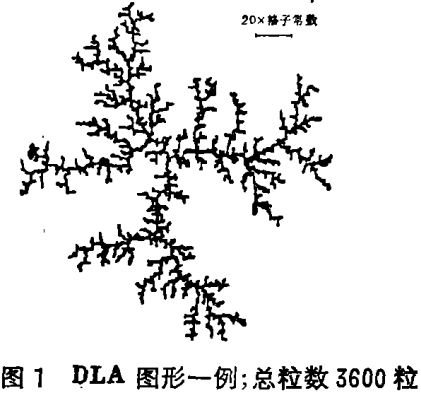
先说明一下模型。仍以2维正方格子为例。将核位于原点,在以核为中心的很远的圆周上随机地选择一点,从这点发出一个作布朗运动的粒子,当这个粒子运动到与核相邻的点时,便附着在核上组成两个粒子的图形。然后再从圆周上随机地选一点,发出布朗粒子,当它到达图形的相邻点时,又作为图形的一点静止下来。如果粒子跑得离图形太远,就舍去,重新选点进行。这样反复进行下去,在原点周围便生成DLA图形。
这种图形具有向周围伸展的大大小小的分枝组成的构造(见图1)。除了粒子大小(格子常数)和图形本身的大小以外,不存在其它特征长度。它具有自相似的特征。这是由于布朗粒子运动的轨迹扩展的非常曲折(轨迹本身的分维为2),因而图形外部伸出的分枝获取布朗粒子的概率较大,妨碍了布朗粒子向图形内部侵入(屏蔽效应),结果图形就按照向外伸展分枝的构造不断生长下去。
在空间维d=2 ~ 6的情况下进行计算机摹拟的结果,图形的自相似性或其分维df都与所采用的格子无关,只依赖于空间维数d,显示出这种普适性。
在解析理论方面,有人则用平均场近似得出这种图形的分维df(d)=(d2+1)/(d+1)。这与计算机摹拟结果非常一致。另外,关于DLA模型,还提出了一些有趣的改进型,并进行了摹拟。例如,设在图形边界邻点上布朗粒子的附着概率在1以下;还有采取在线核或面核上附着粒子凝集成图形的模型等。对后种情况,还导出了更一般的关系,即假定核的维数为dδ,则分维df(ddδ)= df(d)- dδ。这与计算机摹拟结果也非常符合。
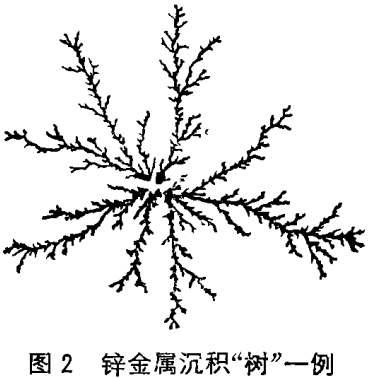
在实验方面,作为2维DLA的一个实例,我们作了锌金属沉积“树”成长实验。在圆皿中倒入硫酸锌溶液,上面覆盖一层醋酸丁酯溶液,然后垂直安放一根细炭棒作为阴极,使它的端面刚好放在两种液体的界面上,在皿的内周安放环形的锌阳极,其间加直流电压进行电解,结果,锌便沿着两种液体的界面从阴极开始二维地析出。这种锌沉积“树”的形状与DLA摹拟图形极其相似(见图2)。不仅如此,只要所加电压及液体温度不超过某一范围,经适当的图像处理求得,所得图形的分维是一定的,不随电压及温度而变化,与上述解析公式所得的维数5/3非常接近。该实验的优点在于,不仅可以一眼看清二维平面上生成的图形,而且在生长速度不太高的情况下,还可以观察到生长过程的细节。实际上,实验显示出在金属沉积“树”生长过程中,正是与DLA相同的那种外枝屏蔽作用使图形实现分形构造这一事实。从而可以断定金属沉积“树”就是DLA模型的一个实例。最近,关于3维电解沉积实验也有所报道,据说也是属于DLA型的。
如前所述,DLA模型是一种在扩散场中粒子凝集图形的生长模型,那么在数学上与扩散场等价的静电场中(都满足拉普拉斯方程)的介质破坏问题也可以归结为DLA模型。关于这种放电引起的介质破坏,尼迈耶(Niemeyer)等人提出过一个模型,但它可以看成是DLA的个别表现。另外,他们还用实验得出了在中的玻璃板上的沿面放电图,与DLA图形很类似。还有,草坪上落雷烧焦的痕迹图也与此相类似,这种雷纹图则是自然界中产生的大规模的平面DLA图形。
另外,在金属沉积“树”实验中,将液体界面上的阴极改为线状,便相当于上述一般解析式中d=2,ds=1的情况。我们用这种实验得出了沉积“树”图形。它与一种叫“树枝石”上的图形很相像,那是由MnO2等物质沿页岩节理面二维地析出形成的结晶图形。于是,可以认为自然界中这种“树枝石”上图形的生长机制也属于DLA题。根据上述在数学等价条件下各种图形的共通性,还可以认为,该实验也是对2平行线间放电引起的2维介质破坏图形的摹拟。
还有一种粘液须毛图形实验。是在间隙很小的两平行板间充以粘性较大的液体,从边缘某一点注入另一种粘性较小的液体。在两液体间表面张力可以忽略的情况下,可以看到一种枝状伸展的须毛图形,可在平板上画出方格来观察图形的成长。虽然这种现象很早就为人所知,但是,在上述条件下,其速度位势满足拉普拉斯方程,故这种图形与DLA等价,这一点却是最近才认识到的。
以上各种实验或自然现象,虽然它们各自生成由来差异很大,但是所得的图形不仅在枝状结构上,而且在分维上都与DLA模型的结果基本一致。可以认为,它们本质上具有共通的物理机制,都是按照DLA机制生成的。可见,DLA的应用范围非常之广,它可以适用于以满足拉普拉斯方程的场为共通条件的一大类图形。
4. 关于KCA模型
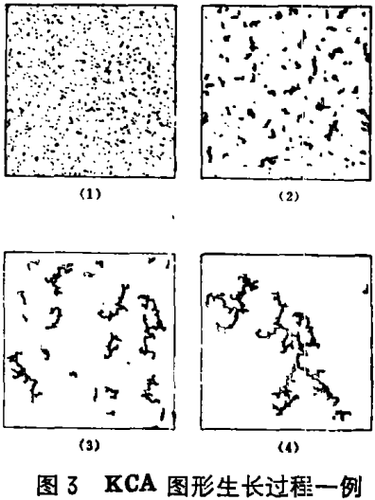
这个模型的摹拟规则如下:按指定浓度分散着的粒子同时开始作布朗运动,当它们中任意两点运动到相邻格上时便结合成一组,这样生成的结合体又以与本身大小相应的移动性继续作布朗运动,当它们与其它粒子或结合体相遇时,又结合成更大的团体,这样不断进行下去便可逐步形成KCA凝集图形(见图3)。这个过程可以看成是诸如:墙角尘絮、豆腐、黄油、河口淤泥、金属超微粒子聚集体等各种分散胶体粒子系统不可逆凝集过程的理想化模型。自然界中有很多凝集现象都属于KCA模型。
在空间维数d=2 ~ 5的情况下,用KCA模型进行计算机摹拟的结果,所得图形都是自相似的,其分维数心只依赖于空间维数d,且比DLA的分维小。这是由于各结合体之间只要有一点相接触就成为一个整体,各自都不发生变形,因而相互不容易侵入对方内部的缘故。由此可以推想,在KCA模型中,各结合体的运动形式(布朗运动)并不是实质性的。实际上已经证实,即使用直线运动来代替各组的布朗运动,所得图形的分维也并没有多少不同。最近我们根据这一事实,以及生长中各组大小比较一致,接近于单分散的假设,提出了一种非常简单的KCA几何模型。根据这个模型,可给出KCA图形的分维为df=log(2d+1)/ log3。虽然还不能认为这个公式能适用到很高的维数,但至少与迄今所作的计算机摹拟结果非常符合。
另外,df与各结合体的运动形式无关这一事实,本身就意味着只用df并不能完全表示出KCA的所有特征。分维是有关生长图形瞬时形状的特征量,它在一定程度上反映出图形的生长过程,正因如此,模型不同所得图形的分维也就不同。但仅仅根据分维还不能完全把握住生长图形的丰富内容。用上述KCA的几何模型可以导出平均粒径
这一结果反映了各结合体的运动状态,所以作为描述KCA模型特征的量,除了df以外,还应当用必威在线网站首页网址
标定指数Z。
近年已出现有关KCA的实验报道。开始是用胶态金、胶态二氧化硅来做的。特别是胶态金实验所得图形的分维与计算机摹拟结果以及上述几何模型所得的理论值都非常一致。目前,我们正在进行这样的实验,即用激光散射方法来测定聚苯乙烯胶乳的分散胶粒通过盐析而凝集成的图形的df和Z。
5. 结语
对于自相似图形的研究,自从曼德尔勃罗特提出分形以来已取得了飞跃发展。但是正如过去偶尔强调过的那样,作为一门超出博物学的对图形的物理学研究,还只能说是刚刚开始。对生长图形的研究时日尚短,生长图形的解析理论更是接近空白,只在DLA类型中能看到它的萌芽。大多数研究都是作计算机摹拟。而实验方面,在DLA和KCA类型中已逐渐开始做出了一些在接近理想化条件下的图形生长实验。
那么,云为什么在那么大的范围内是分形?海岸线为什么是分形?对于河川的分枝、流路为什么会有赫顿(Horton)法则和哈克(Hack)法则成立?玻璃、地面的裂缝又隐蔽着什么奥秘呢?……有待解决的问题真是堆积如山!
[《数理科学》(日),1985年9月]