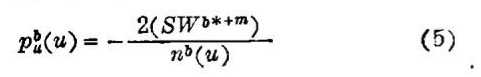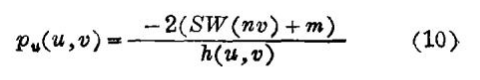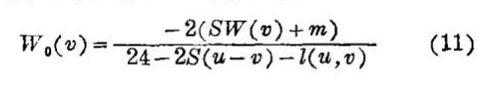本文探讨单中心城市离心型就业模式的居住、工作区位和通勤模型。我们得知,同等家庭依据各自就业人员的工作区位而选择不同的居住区,这就是说,就业人员在中心商业区工作的高收益家庭也许把居住区位选择在中心商业区附近而不是在郊区。这里,收益水平和从中心商业区起的居住距离之间不存在线性关系。同时也表明,同等职工依其各自的工作区位选择不同的居住区位。这一模式认为,企业劳动力的技术构成影响企业搬迁到郊区的积极性。同时还要探讨这一模式的通勤模型。
一、城市集中型就业模式的居住区位选择
当所有就业集中在中心商业区时,首先要简单地一阐述圆形城市理论,假设这个城市位于平坦的平原地区,其中心商业区又是在这个城市的中心点。生活在这城市的家庭都有一个就业职工,并且具有同等的效用函数,这一效用函数取决于住宅对土地的消费,以h表示,其它商品的消费,以x表示,职工的闲暇时间,以l表示,所有这些函数随离市中心的居住距离变动,以u表示,为此,得到这一效用函数:
U=U(h(u),x(u),l(u)) (1)
假设:职工在中心商业区每小时固定工资率为W*,其工作时间是不断变化的;在任一范围里通勤货币成本为每英里m美元,且是个常数;来回通勤货币成本为2 mu美元,时间为2 Su;在距离u的单元住宅土地租金为p(u);家庭受预算制约,职工则受时间制约,一天以24小时计算,分为闲暇、工作和通勤 · 综合以上两种因素为“全部收益”制约因素:
p(u)h(u)+x(u)+ W*p(u)=24W*-2(SW*+m)u (2)
这里,24W*-2(SW*+m)u为全部收益,或职工工作24小时/日,扣除时间和货币通勤支出后的净收益。
明确了全部收益的制约因素,就要对家庭找出h(u)、x(u) 和l(u)的效用最大值。将(2)式代入(1)式得:
U[n(u),24W*-2(SW*+m)u-p(u)n(u) -W* l(u).l(u)]
运用包络线原理对这一效用函数求导,可导出离市中心不同距离区位上的租金曲线的条件,由此家庭在所有居住区位得到相同效用。由家庭住宅租金曲线导出下列条件:
这里,角标表示偏导数
由于工作小时是变动的,工作之余的时间价值便为W*,因而,(3)式的分子表示额外来回英里通勤的总费用,包括货币支出和时间价值。由于(3)式右边是负值,住宅租金曲线必定随离市中心距离的扩大而呈下降趋势。
对u就(3)式求导,并将结果代入(3)式,得到:
住宅租金曲线下降率百分比的变化必然等于减者由居住郊区化的加剧而引起的住宅消费的百分点变化。由于郊区土地租金较低,用于住宅的土地消费就上升,hu就表现为正数,(4)式的左边为负数,所以?pu/ ?u是正数。这样,住宅租金曲线的斜率随u的扩大而变得平坦。
等式(3)叙述了住宅租金曲线的必要条件,这样符合(1)和(2)式的家庭在集中型就业城市的所有区位获得相等效用。而且,如果这些家庭有同样兴趣、收益和一个家庭成员在市中心就业,则市场均衡租金率也必定满足(3)和(4)式。市场均衡租金率为pm(u)。
对这一模式予以引申。假定,家庭仍有同样兴趣,其就业人员一些有技术、一些无技术,前者每小时工资为Wb*。后者则低于Wb*。这样,可得到满足他们各自租金曲线的条件。前者为:
这里,b表示技术职工的家庭的可变值,后者的满足条件也类似,以d表示其可变值 ·
无论是技术职工,还是非技术职工的租金曲线必定随距离的增长而下降、在U点,技术职工的家庭对住宅需求高于非技术职工的家庭,这使其租金曲线呈偏平。然而,技术职工的业余时间的价值更高,这使其租金曲线显得陡峭。一般而言,第一种结果通常被假设为更重要,从两前者租金曲线比后者的显得更偏平。对于在郊区区位的土地的出价,技术职工的家庭要高于非技术职工,而在更中心区位的土地的出价,后者要高于前者。现在两者的差异在于离市中心不同距离的居住区的选址上,而不是在城市的任何地方。
非技术职工的家庭居住在围绕中心商业区从u=0到u'距离的全部范围里的恰当地区,而技术职工家庭则居住在从u=u'到城市边缘u*距离的范围里。特定区位u'是由这两类家庭的居住区的边界。然而,我们不能充分地给出能测定这两种函数式从u'到市中心之间距离相交的截距的模式结构。
二、企业区位选择
令人感兴趣的是,要至少为城市中的一些企业产生从中心商业区迁出的积极性确立一些条件,但是,也要排除许多不存在通勤的郊区企业,因为这些企业的全部职工工作在非常小的家庭企业里,用U表示工作场所区位,按所在中心商业区的任何范围里的英里测算。
假设,这一城市位于平原地区,土地利用未作专门规定,也不实行分区制。企业占有一些但并非全部中心商业区周围的土地。企业支付土地的价格为住宅建设时土地的价值,以pm(u)表示。为取得便利,位于市中心周围的全部企业区位的一些企业,工作地点是允许的,以V表示,为变量并且是连续变化的。但是,对某些部分但并不全部位于郊区的企业,这一模型的一般结果并不会变化。
郊区企业付给其职工的工资取决于其从中心商业区迁出时职工的通勤旅程缩短多少。如果企业迁出后,其职工住在离中心商业区比离企业本身还远的地方,或者同样距离,则企业从郊区化中得到了最大促进,假设,全部职工在郊区找到工作出于如下因素:职工已生活在雇主相关的地区,他们随企业迁移而来,或企业雇用了住在这里的新职工。第一个因素排除了职工向外通勤的可能性,即要求职工生活在距工作场所比离中心商业区更近的地方。第二个因素排除了周期性通勤。对于为郊区工作而乐于向外通勤或周期性通勤的职工来说,雇主要付给他们的多于为同样的工作而在内部范围里通勤的职工。所以,据此找出全部对内通勤职工对企业是有利的。这样,全部职工居住点要比其雇主要远离中心商业区,或者两者以等距离离中心商业区。
假设,所有职工在中心商业区工作,他们有同样技术水平和工资。中心商业区的工资为W*。由于在郊区工作的职工的通勤费用低于居住在相同区位而工作在中心商业区的职工,由此,假设在U>0的雇主支付给其职工的工资要少于在中心区工作的职工。市场工资率为W (u) m,相应的工作场所区位必定是负值,或者?Wm(v)/ ?v<0。
假设,在向郊区区位迁出过程中,企业从中心商业区周围的全部范围里分散出去。这一假设是基于一些企业一旦选址,确切地说,在中心商业区的北部选址,这会阻碍其它企业在同一区位选址,因为所有企业都位于离中心商业区的同一半径的同一区位上,必然会对那些居住在同一半径的职工进行竞争的另一些企业则喜欢在离中心商业区相同的距离内选址,而且以一个层次或更多层次地离开中心商业区的北部区位,那里的潜在劳动资源乐于按工资W (u) m为企业工作的可能性是大的。由于许多企业过多集中于中心商业区的任何一个具体半径范围里而存在一个集聚的经济问题,由此企业会不顾一切地远离中心商业区选址,如果位于某具体半径范围的企业所提供的总的就业岗位大于居住在同一范围里的职工,只要某些职工向外通勤或周期性通勤,那么,企业就能吸引足够的职工。但是,这要求只要这些职工从不同的范围里分散出去,企业就应付给其高于必要的工资,由此,全部职工就能向内通勤。这些假设意味着,郊区次中心不可能容纳足够的企业,这些企业吸纳的劳动资源由为其工作而向内通勤的职工所组成。
应指出的是,企业迁郊严格地受其雇佣职工的劳动力市场的限制。虽然位于中心商业区的职工能雇佣居住在中心商业区任何范围里的职工,但企业迁郊就不然了。位于中心商业区北部的企业只能雇佣居住在中心商业区北部和比企业迁得更远地方的职工。其结果,较小企业对中心商业区迁出具有吸引力。
本文意图,并不在乎描述企业区位决策的一般模式。这一模式会使企业在迁郊过程中获益,因为企业在郊区支付较低的土地价格和工资,但是商品运输成本或生产成本可能较高。在中心商业区周围的每个区位,企业对其区位选择的获益最大化。在这一模式中,假设一个郊区圈线n个,是任何企业获益最大的区位,那么这一假设是合理的。这一假设意味着,同等企业会集中于一个或几个郊区圈,而不是各自分布在所有郊区圈。然而,假使有些企业处于城市中许多产业的企业,则这些企业将位于能使其相应产业获最大化的区位里圈,但应指出的是,假使许多企业位于同一区位,也会导致规模不经济。这样,企业会对这一区位的土地提高出价,从而使其本身产生接近或远离这一区位选址的积极性。这些邻近的区位需求较小,地价较低。如果企业分散于许多区位,那么企业将按用于建造住房的市场租金率支付地价。
三、城市离心型就业模式的居住和工作区位的选择
现在,研究单中心城市离心型就业模式中家庭居住和工作区位选择的问题。这一研究有助于了解离心型就业城市中均衡市场租金和工资变动率的特点。
假设,只有一个人就业的家庭和所有人就业的家庭有同样的技术水平。在离心型就业模式中,家庭对商品和闲暇时间的需求取决于居住和工作区位,分别以u和v表示,其效用函数则为:U= h(u,v),x(u,v),l(u,v)
在离心型就业模式中,存在市场租金变动率,以pm(u)表示,它仅取决于离市中心的居住距离u。换言之,由居住在u点的家庭支付的u区位的土地租金不取决于家庭中就业人员的工作区位。但要考虑以下可能性,在不同工作区位就业的人员的家庭乐于对同一居住区位的土地支付不同的租金。这样,家庭租金曲线p(u,v)就有可能取决于居住和工作区位,如果家庭租金曲线因工作区位变动而变动,则p(u)就会在不同工作区位的就业人员的各类家庭的租金曲线的包络线之上。
类似的是,在离心型就业模式中,也存在一个市场工资变动率,它仅取决于工作场所区位到市中心的距离,换言之,位于离市中心v英里的雇主不论职工住在何处都付给相等工资,但也要考虑如下可能性:居住在不同地方的职工也许乐于为工资水平差异而到特殊的工作区位工作。这样,职工工资曲线W(u,v)也许取决于工作地点和居住区位。假使职工的工资曲线因居住地点变动而变动,则Wm(v)将在不同居住地点的家庭的各类就业人员的工资曲线的包线的下方。由此,家庭的全部收益制约因素可用下式表示:
p(u,v)n(u,v)+x(u,v)+W(u,v)l(u,v)=24W(u,v)-2(SW(u,v)+m) (u,v) (6)
式中,p(u,v)和W(u,v)分别为家庭和其就业成员的租金曲线和工资曲线。由于全部职工向内通勤,通勤距离为(u,v),全部收益为24W(u,v)-2(SW(u,v)+m) (u,v)以F(u,v)表示。
在h(u,v)、x(u,v)和l(u,v)和居住场所u,工作区位v的消费选择的情况下,就可对家庭全部收益制约因素找出效用最大值。全部收益制约因素必须满足全部居住和工作地点。把全部收益等式替代为效用函数,得到:
v[h,24W(u,v)-2(SW(u,v)+m) (u,v)-p(u,v)h-W(u,v)ll] (7)
家庭在他们选择的所有工作和居住地点都必须获得同样效用。利用包线原理就u和v对(7)式进行求导,则得:
24Wu-2SWu-(u-v) -2(SW+m) -pun-Wul=0 (8)
24Wu-2SW(uv)+2(SW+m) -pvh-Wvl=0 (9)
等式(8)(9)分别阐述了离心型就业城市中家庭租金和工资曲线的特征。
首先注意(8)式中的Wu—项。假设家庭住在任意的居住区位u',家庭的就业人员工作在工作区位v',v' ≤u'。在v'工作的职工,其工资必须少于或者等于生活在接近或远离u'的职工在v'得到的工资,由此,Wu(u',v')值必须等于零。对家庭租金曲线求解,得;
再看(9)式的pv一项。假设,职工工作在任意工作区位v″和居住在任意居住区位u″,u″≥v″。居住在u″的职工家庭,其在u″的租金必须大于或等于就业在接近或远离v″职工的家庭在u″的租金。由此,p0(u″,v″)必定等于零。解职工工资曲线,得:
四、通勤行为无差别利润
在存在多层次技术水平且仅在中心商业区就业的城市中,任何收益水平的职工对通勤历程漠不关心。这一特点适宜于从城市最内部到最外部居住区的范围、由于较长的通勤距离可以由远距离的居住区低房价补偿,因此职工对这一通勤距离漠不关心。
这一研究提出了寻求通勤历程变动的离心型城市是否存在类似的无差异特点的问题。事实上)这一特点在离心型城市中更具有普遍性。由于郊区具有同中心商业区工作区位一样的可能性,居住在任何居住区位的职工对从家庭工作场所(通勤长度为0)到中心商业区的工作场所及其到城市的任何工作场所可能表示漠不关心。由工作现场区位的变化所引起的通勤历程的扩大会从工资率的变化中得到补偿;而居住区位的变化所引起的通勤历程的扩大会从较低的住宅价格中得到补偿。对特殊通勤历程的偏好仅存在于具有特殊爱好的家庭,诸如在城市中一般家庭仅有1个就业职工,而这些家庭有2个职工。
事实上,特殊情况下的通勤无差异性已在本文的第3节中作了描述。一般而言,家庭的住宅土地租金曲线取决于其职工的工作区位,不同工作区位的职工工资曲线的变动取决于其家庭的居住区位。这些特点导致了各类家庭根据业就业人员的工作区位而分成若干居住区的居位模型和就业人员根据居住在具体的居住区位对工作选择而形成的工作区位模型。由此,城市就业离心型模式中的通勤无差异性较之流行的城市就业集中型模式范围来得狭窄而不是宽广。在离心型就业模式中对通勤历程的无差异性仅适用于这样的情况,即职工对其选择的居住区位和与工作现场相联系的居住区位之间的所有历程长度将表示不关心。假使有关居住区居住者稀少,那么通勤的无差异性仅适用于狭猛的通勤历程区。由此,不能笼统地说通勤无差异性适用城市离心型就业中的所有通勤行为。
[Journal of Urban Economics,1938年第2期]