低温物理和材料科学最近的进展使得温度极其靠近绝对零度的实验成为可能。如果把所有金属元素冷却到充分低的温度，它们是否不是磁有序的就是超导的呢？本文报告的实验就是要回答这样的问题，为此，贵金属金、银、铜和铂金属铑、靶、铂已在微开尔文温度下进行了研究。

物理学基本原则之一认为，当接近绝对零度（-273.15°C=OK）时，熵必将消失。熵是一个系统有序的量度。零熵就意味着完全有序，按照熵的增加原理，如果一切物质只要足够强烈冷却，它们将转变到熵为零的高度有序状态。转变能够发生在原子无序到高度有序状态中，像液体转变到固体的相变；然而，转变也可能是磁矩高度有序状态中的相变，像顺磁到铁磁的相变，或者表现为动量的有序，像液氦的超流相变或者金属的超导相变。

是否所有物质在足够冷却下都将转变成熵等于零的高度有序状态呢？这个问题的研究是对低温物理学家的一个挑战。低温物理始于1908年［荷兰］莱顿的卡末林 · 翁尼斯（Heike Kamerlingh-Onnes）使氦的液化。氦是沸点最低的物质；它仅在4.2 K（即-269°C）才能液化。翁尼斯在用液氦开辟以下的温度范围后所从事的一个问题是研究在这样温度下金属的电阻性质。出乎极大的意外，在1911年他发现，某些金属在某个特征温度下，它们的电阻完全消失了，它们能无损耗地输运电流。卡翁首先在水银中发现这个现象（由于这一发现，于1913年获得了诺贝尔奖金——译注），后来，在锌、铟和其它低熔点金属中也观察到这个现象。自从巴丁（Bardeen）、库伯（Cooper）和施里弗（Schrieffer）对金属“超导”进行理论解释（于1957年提出的，通常称为BCS理论，并于1972年获得诺贝尔奖——译注）后，我们知道，超导状态是金属传导电子动量和自旋完全有序的状态，即熵为零的状态。

卡翁发现后不久便提出了这样的问题：是否低温超导状态仅仅是一些金属的“奇异”现象，还是很多金属或许甚至是所有金属都能够转变到这种无电阻的状态？

卡翁特别从事研究的金属是金和铂。他在1913年写道：“几乎没有疑问，如果人们只要能获得很纯的金和铂，在氦温下它们也会转变到无电阻的超导状态”。

本世纪上半叶最著名的德国低温物理学家瓦尔特 · 迈斯纳（Walther Meissner）在1925年就已写道：“这是这样一个问题，如果所有金属只要在足够纯状态或者足够低的温度下进行研究，那么是否它们全都是超导的，或者像现有的迹象表明的那样，仅仅有一定的超导金属族”。在1929年迈斯纳又补充道：“目前，看来并未排除以前认为的所有金属在极低温度下是超导的见解。”

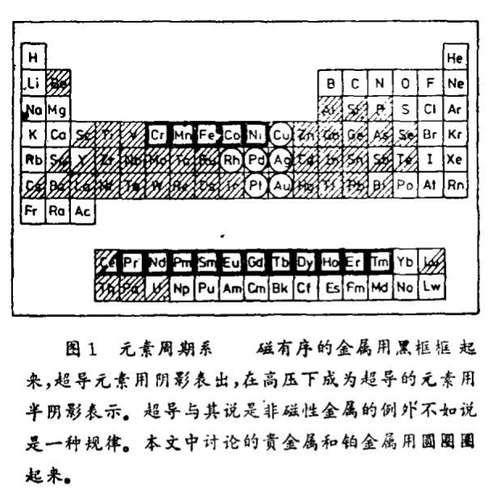
今天有许多超导元素以及超导的金属化合物和合金，然而，是否金和铂以及别的金属在进一步冷却下会变得完全超导这样一个问题还没有最终得到回答。如果用我们今天的知识来考察元素周期系，那么金属元素将被分成三族（图1）：有转变到磁有序状态的金属元素；3d元素（即原子的外层电子的填充是在3d壳层上——译注）铬、锰、铁、钴与镍；以及稀土金属，从铈到铥。因此，有大量的超导金属元素。此外，有一些元素也可算作是超导的，它们在常压下是非导体，例如硅、砷或碲，然而在很高压力下它们就转变成金属导电的，继而在高压下冷却最后就转变成超导状态。超导绝不是一种例外，而常常是非磁性金属中的一种普遍规律。但是，还有一些金属元素，至今发现它们既不在磁性状态也不在超导状态。这首先是碱金属锂、钠、钾、铷和碱土金属镁、钙，其次是贵金属铜、银、金和铂金属铑、钯、铂。

今天材料科学和低温技术的进展使得可以进行极其靠近绝对零度的实验。到1980年，发现相变到超导状态的最低温度，对元素（钨）是T_σ=15 mK心对合金（铱 - 铑）是T_σ=6 mK。在更低的温度，没有发现进入超导状态的相变，因为在微开尔文范围的研究提出很高的实验要求。这些要求自然首先是达到和测量很低的温度，在此温度下进行实验测量，其次是屏蔽磁场对超导状态的破坏，再有是物质的纯度。例如在100 μK时能够转变到超导状态的金属中，超导状态已经为0.001高斯的磁场所抑制了，即是说，我们必须屏蔽明显比0.001高斯更小的值的磁场。然而，更困难的问题还是金属的必要的纯度。由于超导和磁性是两个相反的有序状态，对于有很弱超导状态、仅在极低温度下才是超导的金属，我们必须使其不含有大量的磁性杂质。例如在100 μK左右能够转变到超导状态这样一种金属，最多可以包含的磁性杂质原子的比例为10^-7。这样极高程度的金属纯度，特别是如此微量的杂质浓度的测定，对冶金学提出了很高的要求。

在核研究设施Jülich方面，1977—1979年间我们已经建成利用“绝热核去磁”的冷却方法而实现极低温度的仪器。用这个设施，在直到38 μK这样接近绝对零度的温度下，研究了各种物质的性质。只要当我们强烈冷却金属时，是否事实上它们全都转变到磁的或超导的状态，为了近似得到这个问题的答案，我们来研究铂金属和贵金属在微开尔文范围是否变成超导的。

贵金属铜、银、金

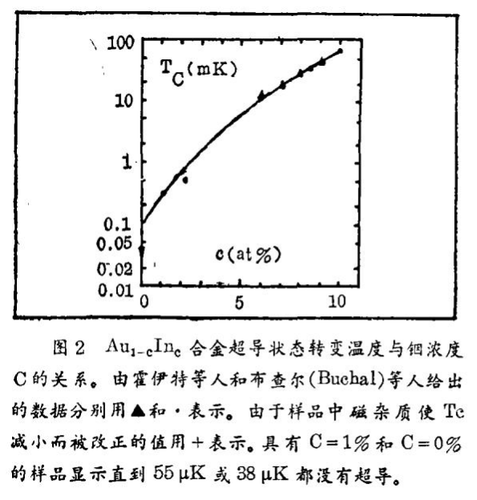
金如已提及的，金是自1911年以来卡翁在低温一下研究过它的电阻的最初元素之一。他以及在三十年代迈斯纳和沃伊特（Voigt）在柏林发现，直到大约1 K温度下金都没有超导相变。1974年伯曼（Burman）和哈尔佩林（Halperin）能够证实，直到0.002 K（2 mK）金都不会出现超导。1976年科隆大学的霍伊特（Hoyt）和莫塔（Mota）作了对我们实验是决定性的预先的研究。他们确定了含有超导元素的金合金转变为超导状态的温度。例如他们发现，由94%的金和6%的铟组成的合金在大约11 mK时成为超导的。我们首先在霍伊特和莫塔所研究的浓度范围内证实了他们的数据，继而把测量扩展到更低的温度和更高的金的浓度。例如，我们能够发现含有97.8%的金和2.2%的铟的合金在0.5 mK（500 μK）下的超导相变。如果我们把图2中铂 - 铟 - 合金的数据外推到纯金，那么纯金在100 μK应该是超导的。然而，直到38 μK在很纯的金样品中我们都没有观察到超导。所研究的样品的剩余阻比大于10000，并且含有的磁性杂质的浓度小于0.1 ppm（即百万分之0.1）。用磁性掺杂使转变到超导态的温度下降，除了与磁杂质浓度有关外，还与它们的性质以及受主晶格有关。对于金在假定的转变温度100 μK时，10^-1ppm（千万分之一）的铁应该仅仅降低10 μK，而为了使转变温度降低100 μK，10^-2ppm的铬或锰就已经足够了。由于我们对于金仅仅期待100 μK作为相变温度，以及我们的样品无论如何总还含有数量级为10^-2ppm或者稍微更多一些的铬与锰的杂质，在这点上可以找到在我们的“极端纯的”金样品中，在38 μK的温度下我们也没有发现超导的原因。我讨论这个例子是为了强调在范围内对固体进行研究时，在许多情况下对材料的要求是极端高的。由于这样的要求，极低温物理工作者是特别乐意从事液氦和固氦的研究，因为那里不存在材料问题。

银和铜除金合金而外，霍伊特和莫塔也研究过银和铜的合金。他们能够证实，银和铜的合金的转变温度明显地位于金合金的转变温度之下，即是说，如果在金中找寻超导都不可能成功，那么在另外两种贵金属中找寻就是很少意义的了。因此，在Jülich设施中我们首先转向寻找一种可能的铂合金的超导。

铂金属铑、钯、铂

在1978年韦布（Webb）及其合作者已经说过，这三个金属直到1.7 mK不会是超导的，在1968年安德里斯（Andres）和詹森（Jensen）已经从铱 - 铑、锇 - 铑合金的研究得出结论，铑的转变温度应该在1 mK或者还要低。按照BCS理论看来，这个结果是出乎意料之外的，因为铂金属固有地有超导态的极好先决条件（高的电子态密度以及导电电子和晶格振动间强的相互作用），根据BCS理论并用铂金属熟知的特性进行计算给出转变到超导态的温度是几个开尔文。然而，至少直到毫开尔文范围内铂金属中都不存在超导，其中一定有一个附加的原因是在超导的BCS理论中没有考虑到的。

下面，我想描述我们在μK范围对柏金属的研究。

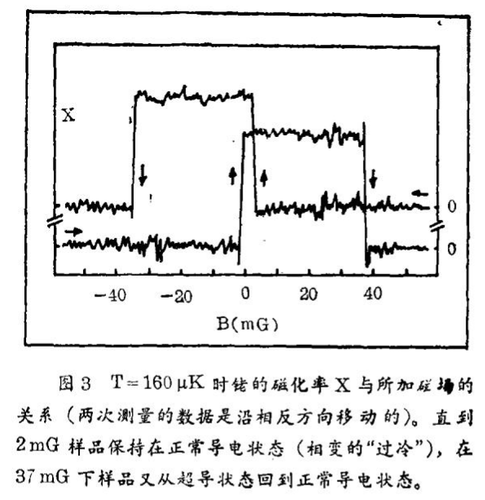
铑对于铑，我们有预期的“非凡的结果”：我们的样品显示了超导，转变温度为T_C=325 μK为了证实这点，我们在很小的场和很低温度情况下测量了铑的交流 - 磁化率。在160 μK温度下测得的交流 - 磁化率随所加直流磁场而变化的关系表示在图3中。如果我们从0.06高斯（即60 mG）出发来减小磁场，那么直到大约0.002高斯（2 mG）的磁场下样品仍保留在正常导电状态，接着出现自发转变到超导状态。然后，如果我们把磁场减小到零，紧接着以相反的符号

又再使磁场增加，那么直到37 mG的磁场下样品都保持在超导状态中；此后，它又成为正常导电的。然后，如果我们又减小磁场，那么直到大约的磁场下样品都保留在正常导电状态，而且此后，一直到37 mG的磁场下样品又在超导状态。按照金的对样品纯度极端要求，在这个结果上指示了对磁场屏蔽的要求，虽然在160 μK下铑有37 mG的临界场，然而在外场中进入超导态的相变是这样一种相变，即它能被过度冷却，而且相变温度愈低，过冷愈烈。铑的转变温度低意味着在这里从37 mG直到几乎1 mG超导过冷能够出现。在这个测量上，如果我们没有把样品上的磁场屏蔽到明显低于的值，那么由于这个强的过冷效应，实验中的超导状态就决不会出现，即铑是保持正常导电的，虽然在37 mG和160 μK的温度，它固有地应该已经是超导的。根据这个发现，铑是具有远为最低转变温度的元素（下一个是钨，T_C=15 mK）。

所研究的铑样品含有大约20 ppm的3d - 金属铬、锰、铁、钴、镍。然而，这里铑的特征还有一半一直没有搞清楚：所列举的元素在掺入铑时失去了它们的磁矩，不再干扰地影响超导。但是为什么铑在开尔文范围内不已经转变到超导态，而仅在微开尔文范围才转变到超导状态呢？因此，为了解释在毫开尔文范围内铑和其它d - 金属没有超导出现，安德里斯和詹森已在1968年作了一个建议：铂金属显示对磁的强烈倾向，例如钯是具有强烈倾向于铁磁有序的金属，但事实上并没有转变到铁磁状态。然而，对磁场强烈倾向意味着，物质中很小区域在磁有序状态短暂的起伏。出现了所谓的“自旋起伏”或“顺磁量子”。这个自旋起伏调节电子自旋平行，而对于超导来说，电子反平行自旋调节是必要的。由于这两者竞争的相互作用，铂金属仅在很低温度是超导的，或者毫不超导。

如果没有磁的倾向和干扰超导态的自旋起伏，铑本来很可能是转变温度大约为已发现的了25 μK以上三个量级的一个超导体。

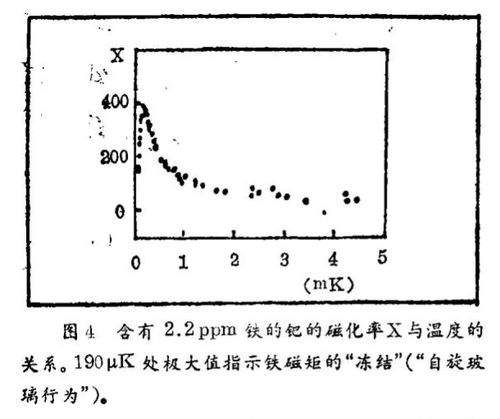
钯如前所述，钯是最强烈倾向于磁性有序的元素，但是还没有达到这种状态。由于钯的高度顺磁磁化率，例如铁这样的磁杂质，在它们周围的钯原子上感应出磁矩。与铑中的铁相反（在铑中铁的磁矩消失了），钯中的铁不仅保留它的磁矩，而且由于周围钯原子的极化而产生一个所谓的“巨大磁矩”。我们实验用的最纯的钯样品含有2.2 ppm的铁。在周围具有极化钯云的铁的磁矩阻碍着钯中的一个可能的超导状态。的确，我们能通过我们在极低温下钯的实验指明，在低温时为铁杂质引起的大磁矩冻结在所谓的“自旋玻璃状态”；这表示在一个极大磁化率中（图4）。这意味着在低温下，大磁矩被“牢固地冻结”在一个方向上。导电电子在它上面的散射也不会引起磁矩方向的改变。由于自旋玻璃冻结，锶中磁杂质对于自旋反转散射是无效的，即它们不再可能破坏超导。但是这就意味着，在自旋玻璃冻结温度克下具有磁性杂质的钯，就能否转变到超导来说，其行为像纯钯一样。由于在自旋玻璃冻结温度直到79 μK之下我们也没有发现在我们的钯样品中的超导状态，由此我们可以得出结论：钯直到79 μK的温度都不是超导的。

铂对于铂，由于冶金学方面的问题，我们没有如此决断而详细的实验，如像用至今所列举的金属能够进行的那样。但是我们仍然相信从我们的研究能够得出这样的结论：在100 μK以上的温度铂也不是超导体。

在与超导体接触的正常导体中的超导感应（“邻近效应”）

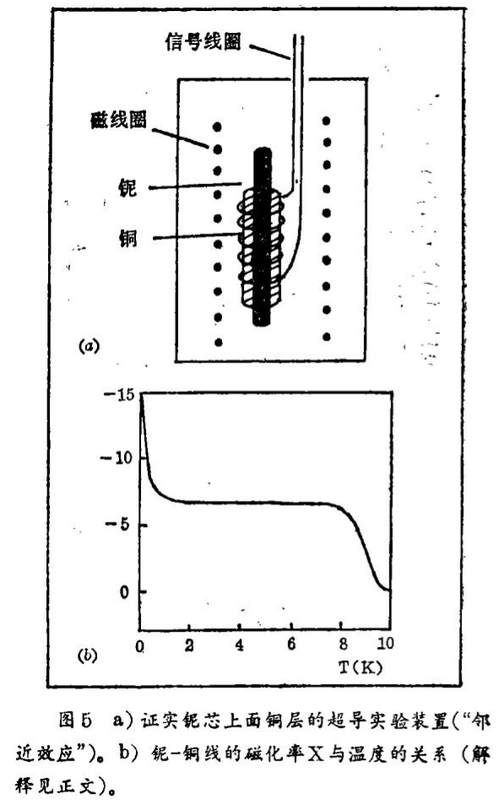
上面我已经讨论、用今天的低温技术和冶金学知识看来是不可能观察到铜中的超导。然而，有一种“技巧”使得正常导电的金属也能够从实验上来研究它的超导特性，为此，使一个正常导电的金属（例如铜）与一个超导体保持良好的电接触。于是，在两个金属接触处附近正常导体—薄层中感应了超导。长期以来，这个效应叫做“超导的邻近效应”。在开尔文范围内，这个超导层的厚度仅是很小的，大约为10^-4mm。然而在更低的温度，在其间感应超导层的厚度能极大地提高。在10 mK，在铜中的厚度大约是0.1 mm。这意味着，在毫开尔文范围内，我们能够研究一个适当的坚实的正常导体的超导特性。1978年奥达（Oda）和纳加诺（Nagano）已经首次证实了在mK范围超导层厚度的极大提高。1983年在拜罗伊特我们已经转向这样的研究。

由十分之几毫米厚的铌芯和0.1毫米厚的铜层所组成的一根丝线上测得的磁化率的性质表示在图5中。

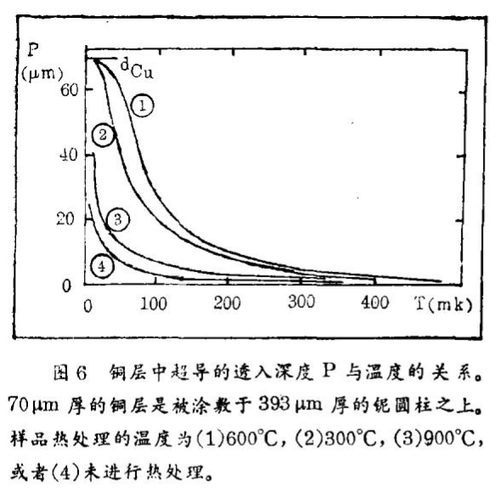
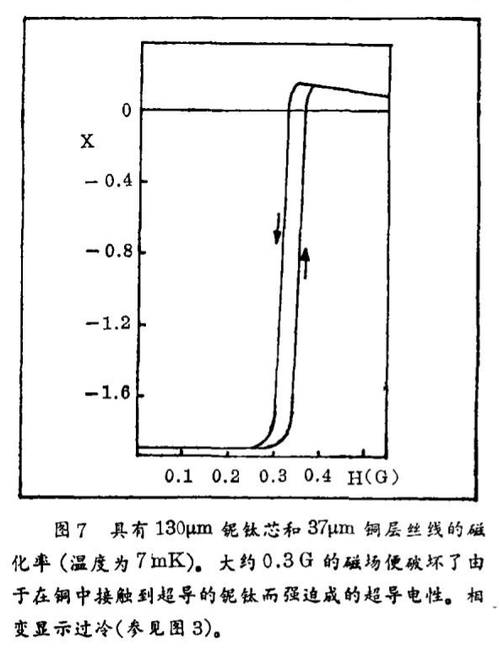
如果铌芯是超导的，那么最初大约在9 K时，出现了丝线磁化率强烈变化。进一步冷却，最初不发生变化，直到最后到1 K以下，磁化态信号又开始变化，由于现在变化缓慢，此时通过与铌的接触在铜中感应的超导出现了。从10 mK与1K之间磁化率信号的变化，我们能够计算出被强迫进入超导状态的铜层厚度。对于许多铌 - 铜线，我们已经求得这个厚度（我们把它称为屏蔽长度，因为像在通常超导体中一样，磁场是在这个长度被屏蔽）。从图6我们能够得知，事实上可以使得400 μm厚的铌芯上的70 μm厚的铜层在大约20 mK时能够成为完全超导的。因此，如果能成功地使铜在超导状态中，那么我们也能测量铜的临界场，即是使得这个超导状态又被破坏了的磁场；为此，一个例子表示在图7中。

结束语

根据上述实验结果，对于卡翁和迈斯纳所提出的问题——如果我们能够制出金属只要足够纯并且足够强烈冷却，那么是否所有金属元素不是磁有序的就是超导有序的呢？我们能够回答说：“或许是这样的”。例如对于铑，我们已经成功了，铑是至今具有远为最低转变温度的金属元素。对于金，也几乎成功了，只是我们必须使金比以前更纯一些。然而，毫无疑义，对于一些金属元素，例如对于铜、银或许还有铂和钯，对于观察一个可能的超导状态来说，低温技术和冶金学方面的要求明显地超出了今天技术的可能范围。这在今后一段时间里还会是这样的，即是说，也许我们在最近的将来也还不能回答所提出的问题，但是超导的邻近效应，即在一个固有的正常导电金属中感应超导，使得我们能够研究那些在今天可能达到的温度和样品纯度下是毫不超导的孤立的金属元素。

[Naturwissenschaften ,1987年第4期]

————————

*夫兰克·波贝尔（Frank Pobell）系［联邦德国］拜罗伊特大学物理研究所物理学家