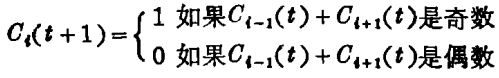一个真实世界的模型到底能有多简单并且怎样才有用呢?在过去的10年里,物理学家和计算机科学家研究了一类叫做“分格自动机”(cellular automata)的数学模型,这类模型非常简单,但它能复制出很复杂的现象。
按常规,现实世界是连续的——时间和空间是光滑的,绝大多数物理量,如温度和质量,可以取任意值。与此相反,在分格自动机里,时间被分成一系列离散的瞬间,空间被分成一种规则的格子,每个格子只允许在一个小的数值集合中取一个唯一的值。这些值通常用一个小整数集合来表示,或者用计算机荧屏上不同的颜色来表示。
在每一时间间隔,分格自动机中的每一格按照一定法则更新它的状态,这个规则取决于格子自身以及邻居现在所处的状态。不同的格子、不同的状态集或不同的操作规则将构成不同的细胞自动机。最简单的是由两个状态一开或闭的格子组成的一些直线。这种一维分格自动机的一种可能操作规则是:
这意味着在时刻t相邻格子的数目之和是奇数的那些格子,在时刻t+1时,将把它们自己转为开的状态,相邻格子数目之和是偶数的那些格子将把它们自己转为闭的状态。
显现这种自动机怎样演化的最简单的办法是逐步描绘出它的相继状态(图1),这里,每一行表示时间间隔。黑格表示格子处于开的状态,而白点表示格子处于闭的状态。其他的操作规则可有不同的行为。对边缘的格子没有特殊的法则,因为大多数格子自动机“围成环形”,因此最左边的格子和最右边的格子是连接在一起的。
第一个研究分格自动机的是数学家约翰 · 冯 · 诺依曼,他是计算机科学的奠基人之一。冯 · 诺依曼想要知道,哪怕是在理论上,机器是否能够复制;换句话说,就是有没有能够自动构造自身复制品的那类自动机。他没有设法用当时的电子管技术去建造一个想象的自动机,而是选择了创造一个简单的模型体系,一个长方形——二维自动机。一个分格状态表示空的或没有被使用的格子,另外的状态(他最终需要另外28个状态)表示构造他的自复制机器的部件。
完全用分格自动机法则控制的机器(它实际上恰好是分格自动机中的一个模式)能把它的手臂伸到自身的每一部分,然后慢慢地来回扫描,创造出它自身的一个复制品。一旦复制完成,它将收回它的手臂。复制出的拷贝又能制造出另一个拷贝,照此进行下去。
从冯 · 诺依曼以后直至1970年,分格自动机失去了活力。1970年,剑桥大学的约翰 · 康韦发明了分格自动机现在最著名的“生活的游戏”。康韦被几条简单法则的组合就能够产生无法预测的可延伸、变形或停止的模式所迷住,他要找出能产生这些有趣现象的最简单的规则的可能集合。
他发现的规则是不能再简化的。“生活”是在一个长方形格子上运转,这与冯 · 诺依曼原来的模型体系相同(长方形格子常用的原因是这种图纸容易得到,而不是理论上的其他性质)。格子中的细胞或活或死。如果一个细胞死了,但它恰好有三个活着的邻居,那么在下一时间间隔它又将得到生命。另一方面,如果一个细胞活着,仅当有两个或者三个活着的邻居时它仍然活着。
自从1970年以来,人们编了很多程序来校拟“生活”。一些程序设计者沉溺于模拟“生活”时所产生的奇怪形式。
事实上,由“生活”产生的模式是如此复杂,以至于证明了分格肉动机与图灵计算机等价。图灵机是一个由无限长的带构成的计算机的一个简化模型,读/写头在非常简单的程序的控制下来回地在带上记录或者消除符号。在30年代,英国数学家阿兰 · 图灵证明了任何想象得到的计算机所能完成的计算他的理想模型也能完成(尽管可能更慢),这说明了“生活”能做的一切,
图灵机也能做,因此,这等价地说明了给定一个适当的初始条件,“生活”的游戏能模拟任何可能的计算机。
最重要的结果是如果不进行模拟就无法发现任意“生活”模式的长期行为。如果是这样的话,我们就能够把同一技术应用到其它和“生活”等价的计算机(包括实际的电子计算机)上去。图灵和澳大利亚逻辑学家卡特 · 哥德尔证明了这样的技术是不存在的,这构成了被称为“停机问题”的计算机科学的基本定理。
在过去的10年里,相同类型的不可预测性成了物理学中的热门话题。考查一类18、19世纪研究的经典动力系统,比如在一个平面上滚动的球。你能用任意时刻t都能求解的微分方程来刻画这类系统的行为。通过对t的值作简单变换,你能确定系统过去任意时刻是什么状态,以及将来任何时刻又会怎么样。
现在考虑在撞球落袋游戏中来回滚动着的球。这个球跳动六次之后它将位于什么地方呢?实际表明这个问题的答案是无法计算的。无论球的初始位置和速度只产生微小的变化,球的每次相继跳动都将会把它放大。由于球的初始条件的微小变化无法度量,因而它的最终位置的不确定性非常巨大。“生活”中存在着与此相同的现象,在一定大小的体系中改变一个单一的细胞,可能有任意大的效果,或者全然没有效果。
具有这一性质的系统被称为“混沌动力系统”,因为一个微小的变化能引起混沌,这类混沌与量子不确定性不相关联——一个弹跳着的球对于量子效果来说太大以至于失去了意义。几乎所有的真实系统都是混沌的,但我们通常是在一些简化的假设下来分析它们,因为混沌在数学上是很难处理的。
分格自动机是一些已知的最简单的混沌系统。即使最简单的如图2d所示的一维分格自动机,它也能展示出混沌行为,这些性质的重要性激发了人们当前对分格自动机产生浓厚兴趣的波潮,这一波潮来自于斯蒂芬 · 沃尔夫勒姆当时在普林斯顿高级研究院所发表的一系列论文。
沃尔夫勒姆用物理学和计算机科学作工具研究分格自动机。他分析分格自动机所使用的第一种方法是将它作为连续微分方程的离散逼近,这就允许他使用热力学的度量,例如熵来描述它们的行为,他使用的第二种方法是将分格自动机刻画为产生语言的机器,产生与不同复杂水平的规范语法规则相一致的模式。
沃尔夫勒姆将分格自动机分为四种类型:类型Ⅰ,模式随时间消失(图2a);类型Ⅱ,模式进化到一个固定的有限尺寸(图2b);类型Ⅲ,模式匀速无限地生长(图2c);类型Ⅳ,模式无规则地生长或收缩(图2d)。
类型Ⅳ包括了那些给出混沌行为的分格自动机,这类分格自动机的初始构形的微小变化就能(但将不是必须的)通过后代进一步传播,直至分格自动机中的每一个格子都受到影响。
由于种种原因,类型Ⅲ的分格自动机是有趣的。这类分格自动机通常产生被称作“分形”的自相似性模式。图2c是那种模式的一个例子。如果我们把这个图形的一个局部放大,它和整个图形有相同的形状,在计算机制图和理论物理等众多领域中,分形还被用来刻画云的外形和空间自身折迭的方式。正如在混沌动力系统中一样,对分形感兴趣的人们正在研究分格自动机,因为它们是能产生这种有趣行为的最简单的系统之一。
虽然分格自动机本身是一个诱人的课题,但人们研究的重点已从对它一般性质的探讨转移到使用它们来模拟不同的物理过程如流体的流动、扩散和晶体的生长的可能性。这些通常叫做“晶格气”的模拟,是通过构造所研究现象的简单模型来使科学进步的范例。
考虑一种流体,例如威士忌。在微观水平上,它是由许多微粒构成,它们通常有不同的形状和质量,微粒能以不同的扩散速度朝任意方向运动。我们可以在微小体积中平均这些粒子的运动来描述它的宏观性质。这产生了一组叫做“纳维叶 - 斯托克斯”的微分方程组。这个微分方程组在原则上给出了流体行为的完整描述,但不幸的是,除了一些最简单的情形外,纳维叶 - 斯托克斯方程组是无法求解的,为了弄清楚实际流体在真实环境中的行为,科学家和工程师们利用实验或者计算机模型来对纳维叶 - 斯托克斯方程组作数值逼近。
显然,在计算机模拟中使用的模型越简单,它就运行得越快(或者说模型在给定的时间内能检验得更多),这就使得研究者们必须回答真实流体有多少属性对流体性质的描述是最本质的。归根结底,像蜂蜜和液态氢这些不同的材料都或多或少地服从相同的流体行为的定律。
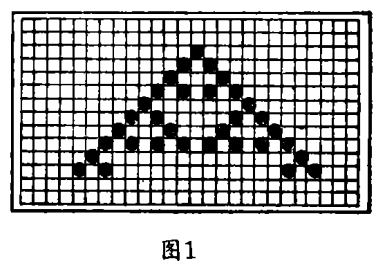
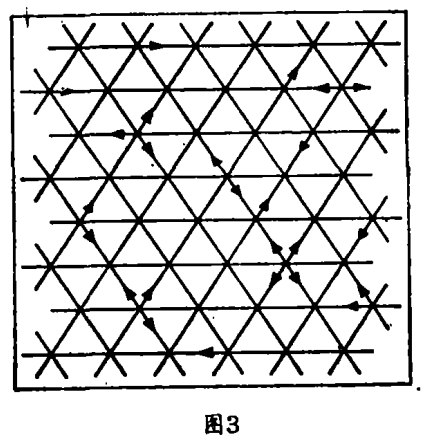
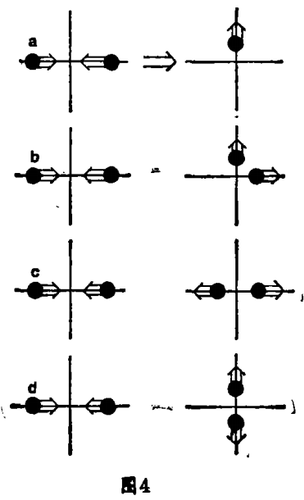
一种晶格气将真实流体的多样性用规则的晶格代替,在每个格子上,相同的微粒只能一步一步地运动(图3),晶格气不考虑真实分子复杂的相互作用,它只按照一些简单规则处理碰撞,这些规则约束在最简单的牛顿物理学之中。质量守恒定律要求进入碰撞的微粒数和离开碰撞的微粒数相同,这就禁止一些规则,如图4a中所示的第一个规则。类似的,动量守恒禁止如图4b中的第二个规则,因为包括运动的速度和方向的矢量和在碰撞前后是不同的。图4c所示的第三条规则在物理学中是不允许的,但在通常的意义上——似乎微粒间全然没有发生相互作用、因而结果相同,这种情形似乎不会产生什么有趣的行为。只有图4d中的第四条规则既“合法”又有用。
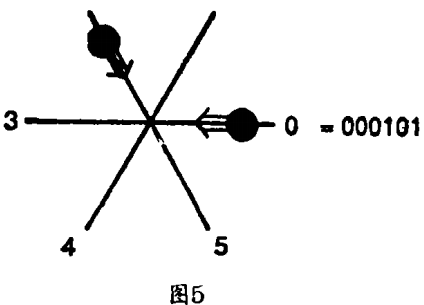
构造晶格气的最简单的方法是使用分格自动机。每一个格点用一个晶格代替,晶格的状态用进出粒子的数目与方向来编码(图5),在每一时间间隔,每个晶格把自己的状态与相邻晶格的状态进行比较,然后确定它十一时刻将处于什么状态——它将有多少微粒向别处运动以及有多少微粒将会到达。可能情形的数目相对来说是小的(在六边形模型中26=64),这还能减少到13。
一旦格子运转起来,我们就能在一大块模拟上平均粒子的运动来计算流体的性质,从而得到那一部分流体的平均动量。如果这个平均过程所得到的结果与纳维叶 - 斯托克斯方程组刻画的结果相一致,那么这一基本模型是有效的。
与此相对,计算机图形学给出另一种晶格气模型,这一模型是布赖恩 · 怀利、理查德 · 肯韦和W. D. 麦库姆在爱丁堡大学发展的。每个箭头表示每边有50个格子组成的平均动量,这个模型是在英国制造的一种超级计算机(Meiko Computing Surface)上运行的,这种计算机采用并行处理。它已进行了如下的模拟:当流体通过有约束的通道时,旋涡由一个倾斜的栅栏产生和扩展,涡流在一根管子的下端形成。
晶格气超过传统技术的优点是容易模拟不规则的栅栏。在晶格气中,栅栏由一组特殊的格子组成,微粒是不能通过这一栅栏的。构成栅栏的格子使用的操作规则与通常的格子所使用的规则不同,它能使进入的微粒以一定角度反射或反弹。这就比试图用一个方程式来表示一个复杂的图形或不规则的波简单得多。
1986年,新墨西哥州洛斯阿拉莫斯的尤里尔 · 弗里希、布罗塞 · 哈斯拉克尔、伊夫 · 波莫证明了必须像图3所示的那种六边形格子。波莫、O. 德 · 帕齐斯和J. 哈迪在70年代所做的早期工作表明像正方形晶格对于恰当地复制流体力学行为缺乏充分的对称性。在大面积晶格上微粒的平均行为不能产生要求的纳维叶 - 斯托克斯方程组。他们在模拟中能清楚地观察到这一效果,在这里栅栏投影自由流动区域而不引起旋流的形成。
另一方面,六边形晶格拥有所要求的对称性。在弗里希、哈斯拉克尔和波莫给出上述证明的同时,能进行大规模模拟的计算机已相当普遍,因此许多研究者开始研究这种模型。
即使微观模型被证明是有效的之后,研究者们在构造晶格气时仍可做出多种选择。一种模拟每次可使用相同的结果(“决定型”模型),或者在几种可能性中随机地作出选择(“非决定型”模型)。虽然后者更符合实际,但它也更昂贵,因为产生一个必须的随机数要比更新一个晶格花费更多的时间。既符合实际又节省时间的模型是“准决定型”模型,在种模型中,计算机根据一个非物理参数选择不同的结果,例如可以根据时间间隔数是奇数或偶数来决定。
对晶格气模型的挑战是怎样将它们运用到三维空间中去。没有一种规则三维格子有足够的对称性来模拟晶格气型的流体。但有一种四维格子,叫做中心面超立方体,它有足够的对称性。我们可以用一个四维格子模拟三维中的流,只须将这个四维格子的第四维取得很薄,然后投影回三维中去。
一个更重要的、仍未解决的问题是如何模拟可压缩流体。实际的纳维叶 - 斯托克斯方程组包含有几项,其中一项描述在任何时刻的温度。当我们导出晶格气模型的宏观行为时,这样的项消失了。流体上压缩的主要效果是改变流体的温度,而这种项的消失意味着分格自动机只能适合模拟不可压缩流体。
晶格气有一个能补偿这些问题的优点,那就是它们很适合在硅片上完成。因为分格自动机中每一个晶格点很简单,以至于工程师们能用超大规模集成(VLSI)技术将成百的晶格点放到一个片上。成百或成千的这种片焊接到一起产生一个“数值风道”,计算机唯一的目的就是模拟空气动力学。这种特殊的硬件早已建造出来,例如在普林斯顿大学由史蒂夫 · 库格尔马斯和肯尼思 · 施泰格利茨所制造。这样的计算机对于设计下一代飞机和宇宙飞船是必不可少的。对分格自动机的兴趣仍在高涨,似乎冯 · 诺依曼的自复制机器已扎下根来。
[New Scientist,1988年10月8日]