熵的基础和它在宏观世界的热力学描述中的意义，在非平衡系统的现代理论框架中进行了讨论，开放系统中的熵产生作为形成“耗散的”时-空结构之源，是物理学、化学、生物学以及有关科学领域中一个基本原理。本文描述熵是如何与演化联系着的，这需要不可逆性、概率和产生新的有序现象的相干性；本文还考察了熵在近代宇宙学模型方西的作用。

熵：一个奇怪的概念

对于现代科学来说，时间和熵是极为密切相关的课题。事实上，爱丁顿称熵是“时间之箭”。熵是一个很奇怪的概念，不可能作一个完备的描述，这里我将着重讲述它的概念性的一些方面。

凡是教热力学的人，在回答学生们的问题上都感到同样的不安，这种不安或许就是我为什么对这个议题变得如此有趣的原因之一。我们常常讨论：“到底为什么要教热力学？”我们可以争辩说；经典力学、量子力学和相对论描述整个的物理世界，如我们所知的那样。假如我们面前的每一件事物都可以用经典轨道或波函数来解释，那么就再用不着熵了。自然，我们能够说：熵对于研究发动机的人是有用的，工程师们应该教熵，但是，对物理学家来说，这不是正确的回答，相反，现今在科学的广阔领域中，熵变得越来越重要；人们说，对于某些含糊的、实际的理由熵是有用的，但是，与之相比，熵还有更深刻的意义：它明显地告诉我们周围宇宙的一些东西。

熵的信息是什么？首先，我们将考虑“我们周围的熵，宏观世界中的熵”，其次，将讨论熵的“动力学基础”，这是形成玻尔兹曼在他整个一生中询问的主要议题；最后，我们将考虑“熵在宇宙学方面的意义”，它使我们想起克劳修斯的最初陈述，即世界的能量是不变的，而世界的熵在增加。在现代宇宙学当前意义下，我们如何理解这个陈述呢？

我们周围的熵，宏观世界中的熵

克劳修斯锻造科学词汇“熵”所引用的希臜词有演变的含义。如果我们讲熵，我们要问：我们是否生活在演化的世界中？

在演化的世界中，至少必须满足三个条件：（1）首先是不可逆性，显然，假如有演化，过去和将来必须是不同的，（2）我们必须引入概率的概念。当我们描述月球的运动时，没有理由说演化是适当的，因为在这里，系统的每一个状态都可以“从刻线（Scratch）”计算出来（不管是在将来或者过去），然而，在天气预报中情况就完全不同了，因为在这里我们只可能提出概率的陈述。（3）我们还需要某种相干性的机制，为了说明在其间有新的、有组织的现象发生的演化的宇宙。

不可逆性是与熵联系着的，对任一给定的系统来说，熵的演化可以分成两个相加的项，一项是由于和周围环境的熵交换，另一项是由于内部的熵产生，对于呈现不可逆过程的系统来说，熵产生总是正的，结果，当没有熵流的时候（如像孤立系统的情况），熵只可能增加并将达到一个极大值。熵产生是和不可逆过程联系着的。虽然全部化学和全部生物学舞不可逆的，然而，经典物理学使用理想化模型使我们能够消除摩擦，因而在这种情况下，一切过程都变成可逆的了。对于化学来说，这是不可行的，普朗克曾经极其强调过这样一个特点了。

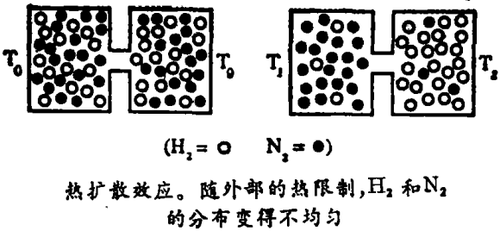
熵产生的作用是什么？它常常有双重的功用：它并非必然地导致无序或废物，它常常是产生有序的一种机制。这点可以从一些极简单的例子上看到，例如热扩散（图1）。考虑一个具有两个成分氢和氮的封闭系统。在均匀的温度下，氢和氮有均匀的分布。假如我们在这个系统上施加以热限制，引入一个温度梯度，那么，我们就将观察到一个浓度（或密度）梯度，在这里，熵产生有双重的效应：它是和产生无序的热流联结着的，但是，它也和“反扩散”联结着，这就意味着有序，因为它产生氢和氮的部分分离。这个双重效应在许多情况下都可以看见，在生物学中，脱氧核糖核酸（DNA）分子的产生是和别的分子的破坏相结合着的。在宇宙学中，我们遇到一个类似的情况，因为我们的宇宙似乎出现一种二象结构，相应于光子对重子的巨大的过剩（大约一个重子对10⁹个光子）。光子显得是“废弃的产物”，而重子是“化石”，即非平衡物体。

简而言之，并非结构是违反熵增定律而产生的。相反，这个定律或许是决定生命和宇宙存在的基本定律。用不可逆性来产生结构是极其类似于我们在城镇中看见的过程。那里，我们有一些不可避免的污染，但是，这仅仅是一方面，另一方面是，有大学、讲演、文化事件、生日庆祝等等。这两个事件是联系着的。你不可能有这个而没有那个。我们常常看不见灰尘或者废杨，我们仅仅注视到结构；于是我们说：这一定是违反热力学定律的。

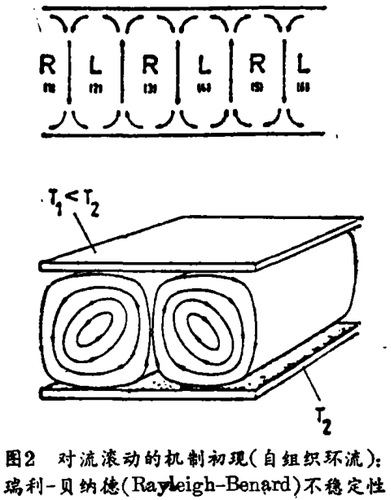
这可以用贝纳德（Benard）不稳定性的例子来说明（图2）。对两个水平板之间的液体层从下面施加以热流。在某种程度上，对于一个充足的温度梯度，相干运动就设立起来了。相干性是刚才提到的三个特点之一；它意味着数百万个分子互相“跟随”。的确，为重力和热流结合产生的这个非平衡稳定状态相应于相干性的机能初现。这是没有预期到的，因为对经典物理来说，有序是和平衡相联结着的（如晶体的情况），而无序是和不平衡联结着的（如湍流的情况）。

过去几年已经目睹非平衡流体中模拟的发展，由于“超计算机”给予的计算功率的巨大提高，马雷夏尔（Mareschal）和克斯特蒙特（Keetemont）最近所作的非平衡分子动力学方面的工作已经得到一些真正显著的结果。下面的水力学不稳定性的模拟，即是关于贝纳德不稳定性，是由一个长方形中封闭着5400个坚硬的圆盘的集合所组成；垂直两边是反射边界，而水平两边是热源。一个外力（类似于引力）向下作用在流体粒子上，下面的热源温度高于上面热源温度。这个模型流体的行为是用计算机在时间上来累计的。十分明显，比较小的系统展示的行为能用宏观水力学来理解。非平衡的条件引起了导致结构形成的长程关联。

由于这些新的模拟而得到有趣的一点是，甚至在平衡情况下也有一个时间之箭。虽然在碰撞前，在平衡状态的分子是不相关的，碰撞产生了关联，继而又消失了。这是不必惊奇的。的确，碰撞机制仍然是同样的，而且毕竟碰撞的分子并不知道它们所属的系统是否处在平衡态。我们甚至在一个平衡系统中看见的时间之箭是十分不曾预期的，因为它好像意味着微可逆性的某种破坏。结局是一个特许的时间方向，相应于顺序［碰撞→关联］，而不是顺序［关联→碰撞］。我们要说，这不是无关紧要的，因为对于一个有限容器中的二体系统，就不是这种情形了。

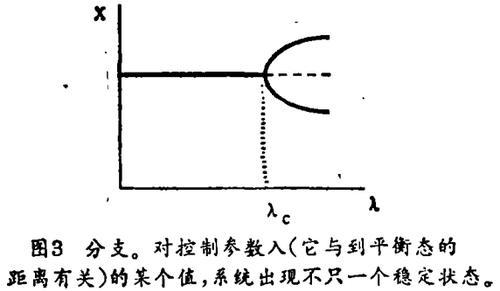
我要强调的另一个方面是概率，当我们来到分支点时，这个方面是很清楚的。远离平衡态，系统进入非线性范围并且展示出对于描述它们演化的方程式的多重解答，在分支点，涨落的作用是决定性的，因为我们不能根据决定论的方程式来预言系统的行为将跟随哪一个分支（图3）。

耗散系统呈现出另一个突出的动力学特征，在于它们具有吸引子。如果我们对一耗散系统施以某种扰动，它可能回到某个参考区域——叫做“吸引子”，并且可以有各种复杂程度，因为系统可以被驱赶到一个固定点，或一条线（像极限环，例如化学钟），或某种更复杂的对象，如像在“奇怪”吸引子的情况中。奇怪吸引子是由一组点构成的，它们有分数（非整数）康。在分数吸引子的情况，系统的行为4初始条件是很灵敏的，并将展示从一个区域到另一个区域的跳跃。

吸引子的研究，在目前是很活跃的研究前沿，特别是因为我们能用适当的吸引子来描述有趣的问题。让我讲述几个用这种方法已经描述过的问题。在长期的气候变化情况下，吸引子的维数大约相应于3.1，这的确是一个小数，当我们考虑到问题的难以置信的复杂性时。在神经病行为的动力学特征中，借助从人的电脑图记录来设计相图，最近已经得到一些显著的结果，这种信号的时间行为清楚地和吸引子相关，它的维数表现出来不是整数，这是混沌动力学的特征。可以证明，对人们不同睡眠程度，相应于（非整数）维度性之不同值。例如，对双眼睁开、醒着的人，关联维度大约是9.7（±0.7），半睡眠状态是8.2（±0.4），熟睡状态是4.4（±0.4）。很有趣，假如某人有癫痫病，那么维度将下降到大约为2。如此，脑的疾病之；一是来自太多的相关性，而不是太少。

我们看到现代科学已经发现描述动力学系统行为的新工具。但是对于别的研究非平衡结构的领域，化学的特殊作用是什么呢？我认为化学使得我们能够看见时间是怎样纳入物质中的，这是特别重要的，因为我们就能描述这样一种世界，其间生物系统的存在就意味着时间现象进入物质的某种记录。水力学不能显示这个效应。例如，贝纳德不稳定性中，一旦你停止了热流，所产生的结构便立即消失了。相反，假如你进行某种化学反应，你可能得到的分子，它们能够对产生它们的非平衡条件保持某种记忆。这是一个不曾被充分强调过的效应。

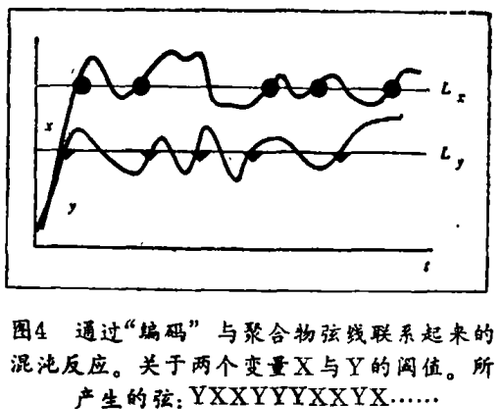
为了在一个很简单的例子中说明这点，我们取两个单分子体X与Y，它们能变换每一个到另一个，或者产生一个聚合物（图4）。每当其中一个呈现出高于某个临界水平的密集度时，这个单分子体就成为聚合物链的一部分，假如我们在近平衡条件下产生这个聚合物，按照泊桑定律，在这种条件下，密集度将剧烈起伏，那么我们将得到一个没有相关性的高度无序的链，如像XXYXYYYXYXYYXXXYX……假如系统的行为相应于一个极限环，那么，显然这个链将多少像XYXYXYXY……在这里我们已经看见非平衡已经纳入聚合物的结构。

这就是说，像XYXYXY……这样一种周期结构，对于产生生物分子来说并不是一个很有希望的候选者。这就是为什么发现尼科里斯（G，Nicolis）和萨巴拉奥（J. Subba Rao）最近所做的工作是很有意义的，其中聚合物产生反应是和混沌反应结合着的。一个链产生出来了，在某种意义下，它是在有序和无序链“之间”，而且X与Y的序列可以用高阶的马尔可夫，（Markov）链来描述。这样的结构有某种“信息内容”，它相应于某种“不可压缩的”一维信息。信息理论的问题之一乃是，为了量度信息的信息内容，我们必须详细说明能够产生这个信息的程序必须有多长。显然，链XYXYXY……中的翻译程序是很短的。然而，假如这个链的确包含某些长程关联，那么你就需要一个很长的程序来产生它；这种情况是更现实的。

这里，我们已经站在把化学和信息理论联系起来这样一个问题的前面，这个问题在曼弗里德 · 艾根（Manfred Iigen）的工作中已被极好地阐述说明。还有很多东西等待去做；但是很清楚，生命是和非平衡情况相联系着的，或许在某个阶段，非平衡状况利用奇怪吸引子来产生信息。所以，我们可以指出，生命是和非稳定性联系着的。我们将看到，在宇宙学中目前的情况是与此十分相似的。

熵的动力学基础

假如掷一个股子或一个硬币，在结局分布中我将发现某种规律性，在抛掷硬币的情况下，就是1/2对1/2。表现在抛掷硬币中的自然界基本规律是什么呢？我们能够说：概率。但是这个回答可能听起来是奇怪的，因为我们知道，毕竟硬币是遵从牛顿的决定论的定律的。对这个两难，现代动力学给了一个很好的回答：为了告诉控制这个系统的规律是磁率性的还是决定论性的，我们必须看看系统的制备。

让我们假定，我们连续地取初始条件，它们是知道得越来越好的。那么两件事情可能发生：对于一定的精确度，我能告诉说，对于初始条件的某些有限间隔，所有结局将是“正”，对于另外一些间隔，它将是“负”，在这种情况下，系统是固有地可预言的，我们的概率描述仅仅是由于我们对初始条件认识不充分。或者就是，导致“正”的结局每一点被导致“负”的结局的点所围绕着，正如对实数那样，每个有理数是被无理数所包围着，反之亦然，在后一种情况下，不管什么样的精确度，都不会给我一个决定论性的结局预言，因为我知道的一切是一个有限的间隔，而有限间隔相应于无限多点数。令人珍奇的是，这种情况就是一大类动力学系统的情况，在那里对初始条件的灵敏性使我们不能确信地预言最后的结局，不管我们的信息的（有限）精度怎样。

这点可以用“面包师变换”来很好说明，这种变换用于一个正方形，代表简单的操作顺序：拉平、切割、折迭。结果，任何两个初始点，无论它们靠近程度怎样，将由于这个变换的重复进行而或迟或早地分离开（图5）。对相空间中点的坐标使用二进制数字，这个散离可以给予一个很好的表示；于是每一次重复变换就相应于这些数字中间的一个“伯努利”移位。这就意味着，为了在我们的关于线性增加的时间间隔预言中确保一定的精确度，我们需要指数地增加初始条件的精确度。但是每一个有限的观察仅能给出一个有限数目的数字，无论这个数目是多少。这种情况是类似于气象学中的情况。预报长时间间隔的天气是不可能的，因为气候的演变似乎相应于很不稳定的动力学系统，其间任何两个初始条件，无论它们怎样接近，是随时间指数地发散的，这就是为什么我们仅能作出概率性预言的原因。

从不稳定性到概率的过渡也导致不可逆性，这是玻尔兹曼研究的主要问题。但不幸的是，当时研究不稳定动力学系统的时候尚不成熟，动力学的描述基本上是限于所谓的可积系统，诸如摆或者牛顿的未受扰动的行星运动，服从于完全的描述，因而是完全决定论的预言。对玻尔兹曼来说，不可逆性只能是由于某些很特殊的初始条件，从新的意义上看来，不可逆性是从可测量性的有限性上表现出来的。我喜欢强调这点，因为它也可能在相对论、量子力学和热力学中发现；不可逆性实在是我们世纪的主旨之一。

为了量度在“经典”物理学极核心中发生的概念性变化，我援引利特赫尔（J. Lighthill）最近一篇标题为《最近认识到的牛顿动力学可预言性的失败》的文章：“我必须以广大的全球力学工作者同行的名义来说，我们愿意集体地道歉，错领普遍的受教育的公众，散布了满足牛顿运动定律的系统的决定论思想，在1960年以后它们被证明是不正确的。”并不是每一天，科学界必须为一个在3个世纪之久都未被注意到的错误道歉。如此，我们看到熵的基本信息是，我们是生活在一个以不稳定动力学系统为特征的世界中。如果我们的宇宙仅仅是由有规则的、时间上可逆的运动（像行星模型或者谐振子）所构成，就不再需要熵、化学或生物学了。过去，熵是一个奇怪的对象，因为人们讲动力学系统的原型是可积系统。的确，对可积系统就没有熵，学生们问为什么要讲熵？”他们是正确的。在新的意义上，熵的学习必须分三个阶段来进行。首先是现象阶段，如包含在热力学描述中。这里主要的新要素是不可逆过程的建设作用。第二个阶段相应于把不可逆性纳入经典动力学中。在这个阶段，我们仍然相信经典动力学，但是我们必须证明不稳定性是如何导致结合着不可逆性的描述。虽然某种进展仍有待于完成，但是现在的第二个阶段是了解得比较好的。还有第三个阶段：应该明瞭，归根到底，经典动力学不是20世纪的概念框架，今天的基本理论是量子理论和广义相对论。值得注意的是这两个理论相应于时间可逆的描述，而为了包括热力学第二定律，它们必须加以修改。

熵在宇宙学方面的作用

时间是如何诞生的？熵是如何诞生的？让我们回忆一下克劳修斯的经典陈述：宇宙的能量是不变的，宇宙的熵在增加。今天如此陈述的意义是什么呢？

在许多教科书中，今天我们可以读到：我们的宇宙是“自由的午餐”（free lunch）。这个说法的意思如下：

能量表现为两种形式，即引力和物质 · 引力相应于一个吸引力，因此相应于负的能量（如果我们稍微深入思考一下，你将发现这是不简单的）；物质相应于正的能量。在真空中，既没有引力又没有物质；比喻的说法就是0?0+0。相反，在其实世界中，我们有两个量之和，一正一负，其总和可以再度为零。这就是“自由餐”的思想。让我们记起贝纳德胞元的水力学不稳定性_这些胞元的价值或者DNA的价值不是能量；从这个观点看来，DNA或者贝纳德胞元就是一种自由午餐。价值是熵！当我们从下面对系统加热时，大部分热流丧失了，但是有一部分用来产生了花样。因此，存在和不存在的差别不是能量，而是熵。宇宙的价值应该付与熵。在我们的宇宙初期，这个价值是怎样被付与的呢？经典图像说熵依时而增加；每一天我们更接近于热死。但这不可能是事情的全部#宇宙目前的“总熵”是用光子总数来估计的，而宇宙的所谓“比熵”是用每个重子的光子数（这个数大约是10⁹）来量度的。这两个数把我们带回宇宙的最初阶段_现在的宇宙的熵是在宇宙开始时产生的。换句话说，宇宙以熵的猝发开始，“热死”在我们的后面，不是在我们的前面，而由于仍然正在恒星和生命层中继续进行的不可逆过程而造成的熵现在的增加，与之我们的宇宙开始的熵产生比较起来，是可以忽略的。

我们想起现代宇宙学是以把时空结构与物质联系起来、用压力和密度表示的广义相对论为基础的。宇宙学的历史极好地说明在科学中时间增长着的作用，爱因斯坦在1917年描述静态宇宙的第一个思想仅仅存在几年，因为很快就证明爱因斯坦的静态解是不稳定的；接着就来到另一个发现：宇宙的膨胀。往后（在1965年）令人极为惊讶地发现：宇宙包含着一个“剩余的”黑体辐射。

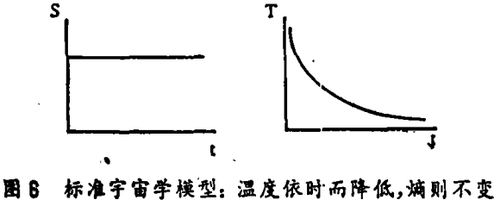
这样，科学界从静态宇宙走向历史的宇宙，相应于依赖时间的几何学，并最后地走向一个涉及固有演化的模型。在70年代建立起来的“标准模型”（图6）指出，当我们走向大爆炸的原点时，温度在增加。按照爱因斯坦的方程式，熵是一个常数，因为这些方程描述一个绝热的演化。这是自然的，因为广义相对论本来就是牛顿天体动力学的普遍化，在行星运动情况下，显然没有熵产生。这不是很满意的，过去几年已经做了越来越多的努力去了解初始条件。宇宙以巨大的熵和量级为10³²的温度（即“普朗克温度”）开始的这样一个初始条件是一个奇怪的出发点，在某些方面已经取得成功的一种理论是“暴胀模型”，就不去多谈了，因为它没有谈及我们在这里感兴趣的不可逆性问题。

我的同事和我本人所提出的模型是基于闵可夫斯基真空不稳定性思想。真空（记住自由餐的思想）在某种意义上类似于过冷液体。假如在过冷液体中出现一个足够大的晶体核心，液体将变成固体。我们的方法指出，情况是多少相似的，如果我们假定在引力和标量物质场之间有一个耦合的话。在真空中，有相应于重粒子出现的起伏（像在过冷液体中）；而且有一个临界质量，相应于普朗克质量的50倍。如果起伏的重粒子达到临界质量水平，那么真空将变成临界的，系统进入一个新相，相应于宇宙，不再相应于真空。在这个方法中，不再有任何的大爆炸，只是某种相变，从宇宙的前驱（“真空”）导致宇宙的早期阶段。

普朗克质量相应于10^-5克，与基本粒子相比，它是巨大的，并且只能是一个黑洞，因为这个质量的康普顿波长比它的史瓦茨半径大约要小10²⁰倍，而且假如质量为m的一个给定物体的大小比它的史瓦茨半径小，那么无论物质还是辐射都不能从这个物体中脱逃出来。

关于我们的宇宙的起源所提出的这个新图景显得是如下的样子，不稳定性导致黑洞的分布。在这个阶段，我们有一个相应于黑洞布居密度是常数的“西特尔”（de Sitter）宇宙，和一个指数增长的宇宙。但是，黑洞有一个有限的寿命。它们在量级为10^-37秒的一段时间以后便消失了。此时，“西特尔”宇宙自身便转变成通常的、绝热演化的“弗里德曼 - 莱麦特尔”（Friedman-Lemaitre）宇宙。

显然，如此一种图景包含着推测的成分。然而，有趣的是，我们能预言宇宙的总熵和重子对光子比的正确数量级。因此，似乎是宇宙总熵大部分是在量级10^-37秒的极短时间内产生的（图7）。在这种新的剖析中“热死”实际上在我们后面，因为熵的这个初始的增加比之以后可能发生的一切都要巨大。这就把我们导致像贝纳德不稳定性同样的情况，具有许多废物和一些不平衡的物体，这些非平衡态物体是很有价值的，因为它们将产生分子，诞生出我们称之为物质和往后的生命那种东西，如此，宇宙学中经典图像一种形式便显露出来了，它指出宇宙开始像是很有序的，熵是慢慢增加的，最后宇宙将遇到热死。在新的图像中，整个熵的大部分是在极短时间中产生的。

这个模型对我来说，似乎是一个相当满意的模型，因为它统一了现代物理学两个基本倾向。一方面，从强烈倾向于统一，即基本相互作用的统一的观点，结果是很好的，因为我们计算现在宇宙的熵，仅用三个基本常数：普朗克常数、光速和引力常数。另一方面，世界的统一图像不能是整个的故事，因为统一的世界将是一个静态的世界。即使方程是高度非线性的，它们仍有静态解，因此，为了演化我们需要某种驱动力，它将是时空与物质间一种不对称关系。时空通过不可逆过程产生物质。物质是一种污染，一种时空的废物。

从能量观点看，时空与物质之间显得没有本质的差别，时空用场来描写，而场可以和物质结合。差别在于熵产生。可能是现今物质起源的黑洞，不仅有质量，而且有熵。基本的时间之箭应该是由于宇宙的物质内容。创造和时间，从一开始就是结合着的。

显然，这里我们是处于科学的前沿，每个月都有关于宇宙诞生的另外图景在文献中出现。再次，假如我在这里提出的图景可以多少更认真地采纳，这是因为从一开始这个图景就通过物质的创造包含了热力学第二定律，还因为它导致了合理的预言。不管怎样，在最基本研究领域中，无论是在生物学中、在量子理论中或者在宇宙学中，我们都看见强调时间、不可逆性和涨落起伏的新观点的出现。

[Naturwissenschaften，1989年第1期］

——————

*艾尔雅·普里高津（Ilya Prigogine）是［比利时］布鲁塞尔自由大学教授，由于创立耗散结构理论，在1976年获得诺贝尔奖，这是他对熵深入研究的结果——译注