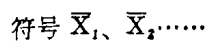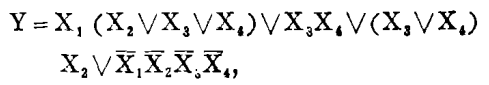值乔治·布尔逝世125周年之际，我们看看他的思想对逻辑学、数学和计算机科学的影响。

在一又四分之一世纪之前，有一个人去世了。按照伯兰特 · 罗素的说法，这个人发现了纯粹数学。知识界的上层大概都熟悉以布尔命名的代数学，即作为现代逻辑学的先驱者乔治 · 布尔是19世纪最有影响的思想家之一。1854年出版的他的名著《思维规律》一书不只对于逻辑学或数学，而且对于尚在诞生的电子计算机科学都揭示了崭新的可能性。那么，布尔的遗产，包括他的思想、方法和发现等对当代科学技术有哪些贡献呢？让我们对他的名著作一快速浏览，名著的全称是“以逻辑学和概率论的数学原理为基础的思维规律的考察”。

从一开篇，布尔就谈到他的著作的抱负不凡的计划：“为了考察用以推理的智力活动的一些基本规律，要用一种运算符号语言给予表示，然后在这个基础上建立逻辑学并创设其方法，……”。在探索过程中他还打算收集“某些关系到人类智力的性质与结构的一些很可能有的暗示”。

对于本质上是一个数学上的问题，布尔使用了非常少的专门术语。他好像是写给有教养的知识界而不只是写给内行看的，他经常引用希腊和拉丁原文的诗作和哲学著作，又偶然从逻辑学转到心理学、社会学或玄学上去。

依照布尔的方法，从事推理的智力活动受制于某种“代数学的”规则，它类似于加、乘等这种常用的数量运算规则。根据这类用数学符号表示的基本规则，他创造了一种解决逻辑学问题的方法。首先以等式的形式提出假设或初始假定，然后用符号的代数运算来代替通常的逻辑演绎过程。于是通过“计算”完成了推理，即逻辑学直截了当地归结为代数学。

诚然，布尔通过“逻辑学”所认识的只是我们现今称为代数类的与命题的逻辑学。但是他必须得到一种全新的方法的支持，这就使现代数理逻辑由之脱颖而出，布尔提出如下建议：“他们通过一般的逻辑规则研究这一问题，同时记住无论有多么复杂都可以无限倍增下去，而且除用这篇论文中的更费力但一定可达到的方法求解之外别无它法”。他还在美学方面为他的方法辩护，主张一种方法的完备不只是根据其效能来评判，还应根据它所显示的一种稍微超乎现代标准的和谐与美感来评判。

布尔将他的演算扩展到命题逻辑，它涉及命题的命题（而不是事件的类），例如，“假如命题Y成立，那么命题X也成立”，等等。他用来对玄学和伦理学上一些经典论证进行分析，发现主要困难在于正确决定论据的实在前提或假设上。只要对此一作分析，并将各个前提表示成符号方程形式，他的运算便不可抗拒地、自动地将他引到逻辑的结论上去。当他注意到这种运算“以几乎可称为机械式的精确性”进行时，方法的这一方面便使他认识到“实际可计算性”的意义（差不多在一个世纪后这个概念才由阿伦 · 图灵使之精确化，图灵机是一种最基本的计算机）。

布尔还讨论了在大学教育中占有重要地位的历史悠久的亚里士多德逻辑系统，目的在于“消除有关其范围和有效性方面的一两个经常出现的误解”。他对于可将所有逻辑推论都归结为一个三段论的说法表示怀疑（典型的三段论是根据命题“全部X都等于Y”和“全部Y都等于Z”，而推论出“全部X都等于Z”）。他认为经院逻辑的真实性太不完备，不足以构成一门学科的基础。

许多年过去了，布尔的创造在许多方面都得以变动、改进和推广，他的原始方案也被一些较简单的系统所代替。但是，他的方法尽管有所不足，其有效性却完好无损，特别他的方法戏剧性地证明了逻辑学如何才能与数学联系起来。

布尔与概率论

与布尔在逻辑学上的工作相比，他对概率论的贡献却未载入史册。最近几乎在70年前考察布尔在这个学科上的思想的是约翰 · 梅纳德 · 凯恩斯（John Maynard Keynes）。这位著名的经济学家在关于概率的论著中善意地将他本人的较为简单的方法与布尔的方法作了对比，还是提到布尔的著作具有高度的独创性和天才。历史学家大概不会由于对概率论的贡献而将应有的荣誉给予布尔。他的某些概念现在都是老生常谈了，从保险索赔到医疗诊断的广大范围之内都已得到实际的应用。

欲评价布尔思想的意义和创见，必须考察那时英国数学界的状况，且不说布尔本人的社会地位和背景了。为了双亲的生计，这位鞋匠之子刚一从公立学校毕业便成为一名教师。18岁时，他已在除基本知识外未经任何数学训练的情况下钻研力学和分析方面的高深的论著了，他通过自学学完了希腊语并基本上学会了拉丁语，同样在自学着数学。几年后，他就在数学杂志上发表论文并由于在分析与微分方程上的造诣而赢得一定的名气了，他的论文“分析的一般方法”作为1841及1844年间最重要的数学论文而获得皇家学会的金质奖章。

1849年，布尔被新建立的科克皇家学院委以教授职位，从而使对他的数学才干的日益增长的赏识达到了顶点。大约就在那时，主要是通过4位英国数学家的工作，使英国的学校对代数学的认识与革新作出了巨大的贡献。这四位数学家是：乔治 · 皮科克（George Peacock）、奥古斯塔斯 · 德 · 摩根（Augustus de Morgan）、查尔斯 · 拜伯济（Charles Babbage）和邓肯 · 格利高里（Duncan Gregory）0但这却使布尔的视野开始从代数学转移到不只牵涉到数字也牵涉到主要是服从结合律的一些抽象的“对象”与“运算”的领域。

另外也必须将另一项成就即不变式的发现归功于布尔。这一发现已由剑桥大学的阿瑟 · 凯莱（Arthur Cayley）和在美国的约翰斯 · 霍普金斯大学及英国的牛津大学任教的詹姆斯 · 西尔维斯特（James Sylvester）等所充分发展。这一早期的代数学研究发展成为不变量的数学理论，它不只在数学之内有重要应用，而且在爱因斯坦的相对论中也有极重要的应用。

布尔的逻辑代数在技术上的应用最先出现在1940年前后，当时美国数学家克劳德 · 香农（Claude Shan-non）将布尔代数应用于分析开关电路。在如电话交换机或铁路信号电路等这类设计用于自动执行复杂控制的各种实用的电气系统中都有继电器接触网络。最初的计算机电路系统也是由继电器和开关制成的，但后来被动作速度更快和更小的元件所代替。布尔代数又是怎么引起人们注意的呢？一只开关的直观的意义是“二者必居其一”。更精确的定义是“某一事物总是处于互相排它的两种状态中的一种状态”。你可用许多方式来具体地体会这两种状态，例如电流或电压的有或无。两种状态通常用0和1这两个符号表示。

现在便能完全决定一个开关电路的运算过程了，归根到底按照规定若干输出开关Y₁、Y₂……Y_m的状态是如何决定于输入开关X₁、X₂……X_n的状态。作为一例考察一下图1a所示的简单并联电路，大写字母X₁、X₂等代表可开（0状态）或关（1状态）的开关或接触点。标着相同字母的开关是同时打开或关断的。

在什么时候都表示开关处于与X₁、X₂……相反的状态。t₁点与t₂点是电路的两个端点。这两点构成另一个“开关”Y，如果电流流过这两点，开关Y的状态就是1，如果电流未流过这两点，Y的状态就是0。因此，此输出开关Y的状态由四个输入开关和X₁、X₂、X₃和X₄的状态所完全决定。可用一个表（见图1b）来说明在16种（=2⁴）可能的输入状态组合下的输出状态是什么。例如表中第一行的结果是基于如下的事实，即假如全部四个输入开关都是0状态（开状态），那么Y就是1状态，因为电流通过了最下边一条分支电路。这样的表就将输出状态规定为输入状态的函数，于是以上开关电路的分析就引出了n个二元变量的双值的即二进制的函数的研究。任何一个这类函数都可以据二元素布尔代数（见图2）的三种运算（或、与和补）而构成。这就可以使我们用一个布尔代数符号方程来表示这一函数（因之也表示了这一电路）。例如，如果“V”是代表“或”的符号，与图1中的电路相关的函数便可用如下的布尔方程来描述：

如果将代表输入状态的字母X₁、X₂、X₃和X₄代入，进行布尔代数运算，就得到了相应的输出状态。这个过程也可以反过来，即根据方程而构成整个电路。

为设计一个特定的电路或网络，首先要列出所必需的布尔方程组，然后通过代数运算或别的方法加以化简。最后，能用适当的零件例如继电器或晶体管来实现这一方程。

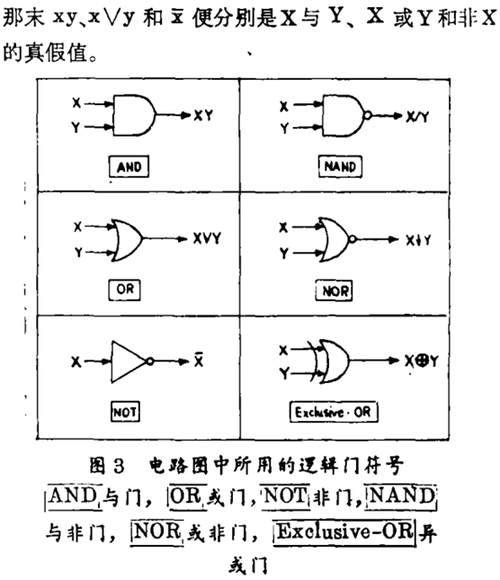
电子计算机是一种典型的数字系统，这便是以数字程序的形式来传送信号或信息的系统。假如我们只用两位数字，便得二进制数字系统。手摇的离散数据计算机为了准确可靠几乎总是二进制的。“逻辑电路”这个词一般是指进行二进制信号运算的电路。这便使我们又回到n个二元变量的二元函数上来，因之又回到综合运用三种基本的布尔运算上来。根据能进行像基本布尔运算或其混合运算（见图3）的一种称之为逻辑门的元件来设置逻辑电路。与图1电路中的接触点不同，门电路不能在两个方向上运算，信号只能从输入端通过而指向输出端。“逻辑电路”中的“逻辑”来源于布尔运算与命题逻辑之间的关系。命题是任何一个可分为“正”或“误”两类的论述，例如“乔治 · 布尔生于莫斯科”（误）；“乔治 · 布尔逝于1864年”（正）。“正”与“误”是命题的两种可能的“真假值”。如果X和Y是两个命题，于是有“X或Y”（逻辑和）和“X与Y”（逻辑积），另外，对每一命题X而言，有另一命题“非X”，即其“否定”。根据规定，上述复合命题的真假值如下决定：

假如X和Y都成立，X与Y便成立，反之不成立；假如X成立，或Y成立，或两者都成立，那么X或Y便成立，反之不成立；假如X不成立，非X便成立，而假如兄成立，非X便不成立。例如，“乔治 · 布尔生于莫斯科与逝于1864年”不成立；“乔治 · 布尔生于莫斯科或逝于1864年”成立，而“乔治 · 布尔未逝于1864年”不成立。假如用1表示“成立”，用0表示“不成立”，那么二元布尔代数（见图2）就变成一个真假值代数问题。图2的两个表中，假如x、y均是命题X、Y的真假值，那么xy、xVy和5便分别是X与Y、X或Y和非X的真假值。

布尔代数应用于电路、数字系统、命题逻辑等一切的基础有一个简单的数学理论：n个二元变量的二进制函数的符号算法。尽管现代数学家和工程师发现了这个有效的现成工具，布尔还是必须把它创造出来。无论他对符号法有多么倾心，且这种方法在逻辑学上得到如此成功的检验，布尔仍忠于一项原则：符号的应用应是达到目的的手段，这目的就是某种可理解的事实或真理知识。他能想到这些符号会有一天也能被机器所“理解”么？他能想到这些符号能够用以表达真正的知识而绝非只是记住事实么？

最后岁月的布尔依然在活跃地进行研究并不断发表论文，奖金、名誉学位和各学会会员等形式的荣誉源源而来。1864年12月8日，他年仅49岁而数学创造力亦值全盛之际，死亡却突然降临。1846年，曾有一首赠布尔的离合体诗，诗的头两行应验了如下预言：

“英雄颂千古，桂冠盖丰碑。”

[New Scientist，1989年8月19日]