流行病学家传统上认为流行病图中貌似随机的涨落是由环境噪声所引起的,而把涨落归于确定性混沌的可能性打开了认识人类疾病的一扇新的窗口。
在大量接种麻疹疫苗之前的岁月里,纽约市麻疹病爆发遵循一种奇妙模式。正如人们所预料的那样,流行病患者在每年冬季达到高峰,那时,孩子们在学校里,人们待在家里,病菌得以传播。但是,二次大战后的二十年里,情况又有所不同。每隔一年的冬季,麻疹病患者急剧增多——经过一个发病率相对低的冬天后,第二年冬天发病率会增加到原来的5~10倍,有时甚至在一个月里有10,000个病例之多。
非常奇怪的是这种两年周期直到1945年以后才出现。从1928年到1945年,麻疹病每年冬季达到高峰。然而似乎没有麻疹病平缓爆发和急剧蔓延的图示。一个发病率相对低的冬季之后是两个发病率高的冬季,反之亦然。纽约市在流行病发病率较低的两年后曾经发生了一场特别严重的流行病,在1个月内,报道了25,000个病例。
始于60年代初的接种疫苗计划结束了这些戏剧性的每年一次的涨落。纽约市的案例一直被教科书引用来作为随时间推移非常神秘地变化的疾病怎样爆发的例子。麻疹和其他儿童病,比如流行性腮腺炎、风疹、猩红热等常常呈现出类似规则性和随机性相混合的图形。
什么原因导致了这样的图形?最近的研究表明其罪魁祸首是混沌,一种貌似随机但实际上遵循确定性规则的奇怪的数学序。基于这种认识,一些流行病学家已经建立了与实际情况惊人相似的预言传染病的模型。例如模拟从1928年到1963年纽约市麻疹病的模型。研究人员指出流行病图形中的混沌及其复杂行为可能对公共健康政策有重要意义,提出了执行接种疫苗计划的最佳方案。
混沌是一个难以精确定义的数学概念。用“确定论的随机性”描述它可能是最好的了。混沌系统是确定性的——它遵循某些看来十分简单的方程——但系统的行为极其复杂以致貌似随机。混沌系统的长期行为不可预言,因为系统初始条件的任何不确定性随时间按指数增加。混沌是被打扮成无序的有序,一只披着狼皮的绵羊。
这种无序的有序(或者也许是有序的无序)已在科学的许多领域中发现。研究人员发现和宣布在化学反应、天气、小行星运动、电磁场中的原子运动、激光、心脏和脑的电行为、动植物种群涨落、甚至在股票市场中发现了混沌。实际上,混沌已变得非常时髦,特别是由于詹姆斯 · 格莱克(James Gleick)所著《混沌》一书获得成功,这本书惊人地畅销。
尽管研究人员已经证明混沌存在于许多系统中,但流行病系统中是否存在混沌仍是一个争论中的问题。
在这场争论中,混沌的最积极的倡导者是亚利桑那大学的威廉 · 谢弗(William Schaffer)。1985年,谢弗和那时也在亚利桑那的马克 · 科特(Mark Kot)公布了纽约市和巴尔的摩麻疹病混沌地涨落的证据。从那以后,谢弗和现在执教于田那西大学的科特与丹麦欧登塞大学的拉斯 · 奥尔森(Lars Olsen)、亚利桑那的格雷格 · 特拉提(Greg Truly)一起分析了密尔沃基、底特律、圣路易斯、哥本哈根、阿伯丁、苏格兰的麻疹、流行性腮腺炎、风疹的爆发情况。他们的工作表明呈现混沌行为的简单的流行病模型能在惊人的程度上重现历史上的模式。
“我们可以得出模拟具有惊人规则性数据的方程”,谢弗说。这项成功的工作导致了他宣称混沌在:沟造流行病图形时扮演重要角色。
其他流行病学家很有兴趣地关注着这项工作。一些流行病学家建议谢弗和他的同事们用混沌解释更多的问题。约翰 · 霍普金斯大学卫生和健康学院的琼 · 阿伦(Joan Aron)说:“我认为他们处理模型太呆板,在流行病中发现了混沌的主张也太武断。”
这场争论的根源在流行病数据的本质问题上。这些数据通常呈现出明显的规则性,例如,纽约市冬季出现高峰球是呈现出两年周期的高/低涨落,但是同时也伴随着不规则性,如纽约市数据的峰值是每年变化的。传统的方法是假定这种不规则性来源于“噪声”——如人口迁移和天气变化这样不可预言的随机事件——而在一个没有噪声的理想世界里,传染病的图形将是十分规则的。
尽管关于混沌在流行病中所扮演角色的争论似乎是相当技术性的。但对我们能在多大程度上掌握和预言传染病爆发却有着深远意义。如果把传染病的涨落归于混沌,则与以往的认识相比,这种涨落具有更复杂的结构。掌握这种精致的结构有助于预言像接种疫苗计划这类事件的结果。
如果涨落果真是出于“噪声”——大量人口的随机涨落——那么预言传染病的发展将更加困难。预报将最终依赖于掌握和预言噪声的来源。
大多数流行病学家(不论是否相信混沌)都用同样的流行病模型做研究。儿童传染病的基本模型是所谓SEIR模型,把人群分为四类——易感的(S)、显露的(E)、传染的(I)和有免疫力的或痊愈的(R)。这个模型的简单的微分方程涉及到每组人数怎样随时间变化,同时考虑了出生率和死亡率、传染病的平均潜伏期和平均传染期。
这个模型的一个重要参数是接触率,或者易感人群的平均数。许多模型中的这一参数在一年之中涨涨落落,反映了这样的事实:人们在一年之中的某些时期(冬季)比其他时期容易染上流行病。
流行病学家传统上研究这些模型的简单、规则解。在产生与纽约历史上从1945年到1963年的按两年周期高/低涨落模式相似的麻疹病模型中,选择参数相对容易些。但是由于这些简单解太规则,流行病学家认为模型中需加入一点噪声——出生率的变化、传染病人的随机迁出或迁入、天气的变化如一个让人们比平时更多地待在家里的特别寒冷的冬天。
谢弗和他的同事们已经表明产生不规则的传染病图形,噪声并不是必霃的。使用SEIR模型,他们已得出麻疹病的计算机模拟,与实施接种疫苗计划之前纽约市的情况十分相似。一些图中呈现出近似的两年周期,其峰值从一个周期到另一个周期不断变化,其他图是跳跃式的,难以预言,其高峰和低谷点缀在一个貌似随机的序列中,这些图的确是混沌的。
如果混沌模型是正确的,其现实意义在于解释流行病的许多行为时将不再依赖于随机因素。在分析流行病图时,噪声总是一个现实事实,但它将不再扮演重要角色,正如谢弗所说:“对于以前无法解释的变化,如果我们把复杂性看成是确定论的便豁然开朗了。”
在他们的模型中,谢弗和他的同事们直接从历史上和医学上的数据中估计出生率、死亡率、平均潜伏期、平均传染期的数值。接触率在一年中是变化的,必须间接估计。然而大量的关于模型与现实世界是否相符合的争论都出在这里。
阿伦承认“这些模型的确呈现出与他们正在研究的某些流行病惊人地相似的图形”,“但是不是其他方法也能做到这样呢”。阿伦争辩说这些模型对某些参数像接触率就极端敏感,如果这些参数在30年或40年间发生较大变化,那就可能产生涨落。
谢弗的答复是在没有混沌的模型中增加这样的变化并没有产生与历史上的数据相符合的图形。他说:“混沌假设提供了较好的解释。”
海军研究实验室的应用数学家艾拉 · 施瓦茨(Ira Schwartz)持与阿伦相似的保留意见。他指出由于报道的变化及其他因素,有效的数据很贫乏。虽然他承认SEIR模型展示了混沌,但他说由于模型做了许多简化假设例如假定人口不变——这未必就与真实世界定性地相一致。“的确存在模型定性性质与数据相符合的情况”,施瓦茨说,但谢弗“企图把模型与他所看到的紧密联系起来”。
谢弗回答说:“我们知道方程并非尽善尽美,所有的模型都是理想化的。我们所希望的是从这些简单模型中产生的状态序列与真正正确的方程所得到的尽可能接近,而且希望这是有用的。”
最后,争论变成了技术性的。施瓦茨强调他没有扮演海军研究实验室代言人的角色,他争辩说谢弗用于模拟接触率中季节变化的参数比数据所提供的要大,谢弗回答说:“在现实的流行病中所观察到的季节性至少必须大到使得系统“接近混沌”,而且这样做得相当好。“如果你拿来一个接近混沌的系统,很小的扰动就能将它激发起来,那么它的行为就不能与真正的混沌有效地加以区分”。
理论上,通过计算某些技术性的数据的特征量,例如李雅普诺夫指数和分维,可以区分噪声所导致的涨落和真实的混沌。如果存在混沌,这些数值就有确定值,否则没有确定值。
虽然数据的噪声降低了计算的精确性,但是谢弗和他的同事们还是计算了几套历史上数据的特征量。在此基础上,在最近的一篇论文中,他得出结论:哥本哈根的麻疹、流行性腮腺炎、风疹表现出混沌,而水痘是简单的一年周期,对百日咳和猩红热,计算结果没有作出定论。
尽管谢弗承认流行病的数据还不足以完全平息这场争论,但他主张做一个有说服力的例子,把非常逼真的摹拟真实流行病的混沌系统与具有混沌标记的数据合并起来。“我小心翼翼,不作站不住脚的结论,但我认为这项流行病学的工作是严肃的”。
不论流行病学中是否存在混沌,简单模型产生复杂流行病图形的认识已经促进了研究人员用新的观点去看待预言流行病的问题,只要认为图形是由随机因素形成的,那么使用今年的数据预测下一年流行病的爆发几乎是没有希望的,但是如果认为大量的表面上的随机性是确定性的,则其行为在一定程度上是可以预测的。
“我确信可以对来年的情况作些预测”,谢弗说,但限于某些年份。在传染病相对少的一年里,下一年任何情况都可能发生。但是对于那些发病率居中或很高的年份里,第二年的情况是可以预报的。
预言普通流行病发展的同一模型能估计各种接种疫苗方案实施的效果。正是在这里,这项流行病工作被证明是有很大的现实意义。
例如,在怀孕期间由于接触而染上风疹的母亲所生的婴儿中,先天性风疹综合症导致了生育缺陷。为了防止先天性风疹综合症,一些国家努力在孩子上学之前尽量给他们接种疫苗,希望能使整个民族完全免疫。流行病学家把这种方法叫做美国战略,英国战略则仅仅给11—14岁的女孩接种疫苗,这已在很多欧洲国家推行。这允许许多孩子患风疹和取得天然免疫力,然后通过给接近生育年龄的女孩接种疫苗来增强天然免疫力。长期的计算机模拟发现被接种疫苗的人数低于目标组的80%时,英国战略比较有效,而其比率增大时,美国战略更加优越。
虽然预测接种疫苗计划的长期结果相对容易,但短期结果却敏感地依赖于计划怎样实施。例如,美国实施接种风疹疫苗方案后的几年里,由先天性风疹综,症导致的生育缺陷的发展实际上是跳跃式的。
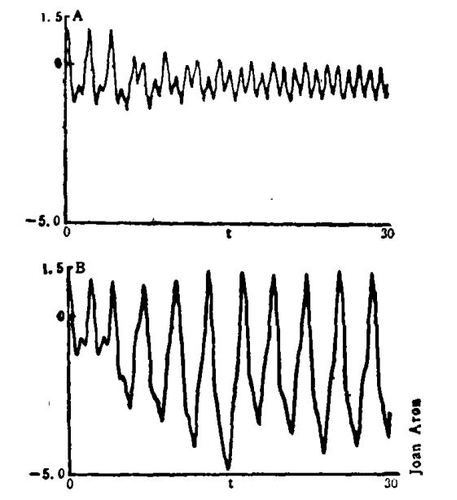
施瓦茨和阿伦阐明了在确认结果时,接种疫苗方案的实施时间是极其重要的,其中一个最令人震惊的结果来自阿伦。她调查了给一种疾病接种疫苗的结果,这种疾病的图示具有高/低交替的两年周期,她发现给三分之一新生婴儿接种疫苗的时间戏剧性地影响了传染病图。如果在发病率低的冬季到来时播种疫苗,流行病逐渐地降为一年周期。其冬季峰值相对较低。但是如果在一个发病率高的冬季到来之前接种疫苗,其结果是三年周期,每第三年流行病暴涨,另外两年则平缓爆发。
实施接种疫苗计划的结果依赖于实施时间是在发病率低的一年(A)还是在发病率高的一年(B)。(垂直刻度是传染病患者数目的对数)
尽管阿伦的工作避免了混沌解,但是它表明了混沌对于流行病学的影响。直到最近,研究人员仍把自己局限于模型的简单解,以为复杂解既难以处理又对现实世界没有用处。这项混沌的工作消除了一个心理障碍,表明流行病图的复杂行为是可以进行并不复杂的数学模型的分析的。
[Science第243卷,1989年1月6日]