

欧内斯特·卢瑟福在加拿大麦吉尔大学讲学。这幅淡彩画系马修斯(R. G. Matthews)于1907年,即卢瑟福宣布他发现了原子核的4年前所作
1911年3月7日,欧内斯特·卢瑟福(Ernest Rutherford)出席一个由曼彻斯特文学和哲学学会召开的会议(早在一个多世纪前,曾任该学会会长的约翰·道尔顿(John Dalton)就提出了测量原子重量的方法)。在这次会议上,卢瑟福宣布发现了原子核。为此,美国物理学会决定把这一天作为基本粒子物理学世纪的开端。
我认为这是一个明智的选择。一方面,在实验中卢瑟福奠定了他有关原子核的结论,并在他的指导下,汉斯·盖革(Hans Geiger)和欧内斯特·马士登(Ernest Marsden)完成了一次自打粒子物理学成为专业以来堪称典范的散射实验。盖革和马士登没有采用加速器产生的质子束或电子束,而是采用从镭的放射性衰变获得的α粒子来观察轰击金箔靶标后发生的变化。他们不用丝极室、火花室或气泡室来检测散射的粒子,是采用涂有硫化锌的屏幕――后者被α粒子击中时会发出一道闪光。
更重要的是,对α粒子在大角度下弹性散射的观察让卢瑟福坚信原子的大部分质量和正电荷都集中在微小体积的原子核内。而在此之前,通常都认为原子像布丁一样,原子中的电子则像嵌在正电荷平坦背景中的葡萄干。原子核的发现,是一系列进展的必不可少的第一步,从尼尔斯·玻尔(Niels Bohr,曾是曼彻斯特卢瑟福实验室的访客)到路易斯·德布罗意(Louis de Broglie),再到埃尔温·薛定谔(Erwin Schr·dinger)和维尔纳·海森堡(Werner Heisenberg),他们引领了现代量子力学。
理论和实验的障碍
在获得量子力学的初步成功之后,基础物理学仍然存在着两个显而易见的尚待解决的问题。一个是相对论现象的量子力学扩展。保罗·狄拉克(Paul Dirac)的处理方式是将薛定谔波动方程推广为相对论波动方程,这似乎是在预测基本粒子必须有1/2自旋(以普朗克常数单位h为单位)方能获得巨大的胜利。但今天我们知道,这个预测与其说是成功还不如说是失败。既然有像W和Z这样像电子一样基本的带一个单位自旋的粒子,我们中的许多人就会想,那么不带自旋类似的基本粒子也会在大型强子对撞机(LHC)中找到。
此外,将狄拉克方程概括成含有超过一个电子的系统是很困难的,未来应该属于通过各种合作而发展成的量子场论,参与合作的包括马克斯·玻恩(Max Born)、海森堡以及帕斯库尔·约尔当(Pascual Jordan,1926年)、海森堡和沃尔夫冈·泡利(Wolfgang Pauli,1926年),以及泡利和维克托·威斯科夫(Victor Weisskopf,1934年)。威斯科夫有一次告诉我,泡利力图在其1934年的论文中说明,在构建一个非常合理的零自旋粒子理论时,狄拉克关于1/2自旋是必要的观点是错的。量子场论的首次应用是用在恩里科·费米(Enrico Fermi)1933年提出的β衰变理论上,迄今它已成为所有成功的基本粒子理论的数学框架。

这张航拍照片显示了LHC 27公里的圆周以及若干LHC实验场所、将往LHC中注入质子的超质子同步加速器 (SPS)
另一个尚待解决的问题是原子核。巨大的障碍来自于库伦势垒(Coulomb barrier),它阻碍了卢瑟福实验室里镭的α粒子进入原子核。这是由库仑斥力所产生的问题,并引起人们最初发展粒子加速器的念头。
在上世纪30年代,对这些问题探索所获得的进展却被理论家一次意外的勉强提议的新粒子所打断。这里有三个例子可循:
第一个例子,詹姆斯·查德威克(James Chadwick)1914年发现,β衰变中电子具有连续谱。而如果电子夺走了核跃迁释放的所有能量,则人们并不期望会产生这样的连续谱。这是如此令人费解,以致玻尔提出在衰变中能量可能不守恒。泡利在1930年提出的中微子的设想遇到广泛的质疑,直到四分之一个世纪后中微子被发现,这事才算了结。
第二个例子,狄拉克首先想到,他的理论负能量电子大海里的空穴必然是唯一已知带正电的粒子质子,尽管事实上原子中的电子可能已经落入这些空穴中,表现出所有普通原子的不稳定性。他随后改变了他的想法。但1932年卡尔·安德森(Carl Anderson)和帕特里克·布莱克特(Patrick Blackett)在宇宙射线中发现了正电子,给了大多数物理学家一个惊喜,包括安德森和布莱克特本人。
第三个例子,为了赋予原子核以适当的质量和电荷,物理学家起先假定原子核是由质子和电子组成,即便这会使氮-14原子核成为一个费米子。而我们已经知道从分子光谱角度看,它是一个玻色子。在查德威克于1932年发现中子之前,中子的概念一直没有被人们接受。
过去在提议新粒子方面,即便是有明确的理论需求也勉为其难,时至今日这已显得不可思议。今天,如果一个理论家还没有引入至少一个还没有实验证明的新粒子,那他或她就很难受到尊敬。1935年汤川秀树以极大的勇气提出,在核力的已知范围内,应该还存在一种质量只有质子质量十分之一左右的玻色子。
与此同时,中子和质子之间相似质量认为存在某种对称排序关系。1936年质子-质子间的核力被默尔·图夫(Merle Tuve)及其同事测得,发现与已知的中子-质子力类似。几乎同时,格雷戈里·布赖特(Gregory Breit)和尤金·芬伯格(Eugene Feenberg),以及本尼迪克特·卡森(Benedict Cassen)和爱德华·康登(Edward Condon)断定,具有对称关系的中子和质子是保持同位旋(isospin或isotopic spin)的组,数学家称之为2阶特殊酉群,记为SU(2)。
二次大战后,粒子物理学得以复苏(在这里我不打算对进行这项工作的物理学家一一具名,因为这样太费时间。我还担心我可能会漏掉某些尚在人世的人)。在上世纪40年代后期,量子电动力学中无穷大的老问题已被重整化理论所解决。汤川提出的π也被发现,与具有类似质量的粒子μ子不同,后者于1937年发现。带有新量子数――奇异性――的粒子于1947发现。所有这些新的粒子都发现于宇宙射线中,但在上世纪50年代,粒子加速器开始代替宇宙射线作为工具来探索新的粒子。加速器开始变得越来越大――它们不再放置在大学物理系大楼的地下室,最终移到了室外,成为一个可以在空中俯视的地理景观。
构建场论的障碍

用摄影感光乳剂捕获的一幅早期介子图像:通过宇宙射线碰撞而建立,介子从右下方进入,稍作停留,衰变成一个μ介子和一个中性的(因而是不可见的)中微子。μ介子继续从底到顶,衰变为一个电子和一个中微子。在高能粒子加速器开发以前,宇宙射线是发现新粒子的最丰富的来源
量子电动力学的显赫成功自然使人们对创建一个将所有基本粒子及其相互作用一网打尽的全面的量子场论充满希望。然而,这一过程布满障碍。一方面,如此一个量子场论将要求选择这样的基本粒子:它的场应当出现在理论的拉格朗日函数(Lagrangian)中。尽管有这么多的新粒子被发现,然而也不可能认真选择其中任何一小部分作为基础。此外,很容易想象任意数量的强相互作用的量子场论,但又有谁与它们打过交道呢?强相互作用是强大的――太过强大以致不能应用微扰理论。一所理论家所在的学校甚至完全放弃量子场论,至少是放弃强相互作用,仅仅信赖S-矩阵――即所有散射过程的一组概率振幅――的一般属性。
对于其他的问题,我们应该用像同位旋守恒这样的近似对称、或自发破缺的“手征”SU(2)×SU(2)对称(它表示低能介子的属性),或更近似的SU(3)和SU(3)×SU(3)对称性(它联系着更大的粒子家族)来做些什么?甚至空间的守恒和时间反演以及电荷共轭(P,T,和C――即宇称、时间、电荷)原来也是近似的。如果对称性是大自然简单性的表现,那么近似的对称就是大自然简单性的近似表现吗?
对于弱相互作用,我们有与实验吻合良好的量子场论――费米1933年提出的β衰变理论,以轴矢量流来补充矢量流概念。但是,当这一理论超越了最低阶的微扰理论时,它给出无穷大,显然无法从重整化中去掉。
标准模型
由于20世纪60年代和70年代基本粒子量子场论即标准模型的进展,所有这些障碍均被克服。标准模型基于概括了电动力学规范不变性的精确对称性。这些规范对称性有些是自发破缺,有些则不是。LHC将确实无疑地为我们揭示这种弱和电磁相互作用规范对称性破缺的机制。基本粒子的选择很明确,它们必须出现在标准模型中――夸克、轻子,以及规范玻色子――然而仍难以计算出由感触到强相互作用的夸克构建强子的最佳份额,但在高能状态下强相互作用的弱化能计算足够多的事项以便让我们知道理论是正确的;以及更进一步,低能量状态下强相互作用的增强很可能说明了为什么不能观察到孤立的夸克。
简单性是通过重整性的条件而施加于标准模型的――拉格朗日函数只可以包含有限数量的基本场项,其中只有有限数量的时空派生物存在。需要有这样的限定条件以便将在微扰理论中遇到的所有无穷大都通过对拉格朗日函数中限定数量的常数重新定义而消解掉。
这种简单性为强相互作用的难以理解的近似对称――比如同位旋守恒――提供了一种自然的解释。理论的强相互作用部分不能太复杂而违背对称性,除了由最轻夸克的质量而产生的微小影响外。同样,理论的强相互作用和电磁相互作用也不能太过复杂而破坏对奇异性及其他特性或(除了某些难以捉摸的量子效应)P、T和C的保持。
并非最终的定论
这显然是要超越标准模型了。夸克和轻子的质量都有一个难以捉摸的频谱以及混合角,对后者我们已经盯了几十年了,仿佛它们是出现在一种未知语言中的符号,因为我们还没有能力来解释它们。此外,对于宇宙中的暗物质,我们还需要有标准模型以外的东西来解释。现在人们普遍认识到,这个标准模型只是一个有效场论,是某个更基本理论的低能极限。后者所涉及的质量范围远大于我们所熟悉的质量。这意味着我们应该期待标准模型以非通常意义下的重整化相互作用――事实上,是以对称原则所允许的所有相互作用――来补充。但是,要通过将分母与新增大质量的次方成比例来进行抑制。无穷大在理论常数的重定义中依然受到关注,但需要重新定义的常数个数不再受到限制。
近年来我们已经找到证据,在1016 GeV附近存在新的质量尺度。标准模型重整化的相互作用和轻子数使重子数和轻子数自动守恒,但没有理由认为,这就是绝对守恒定律。事实上,微小的中微子质量的发现表明,标准模型必须以非重整化的相互作用――即并将抑制在1016 GeV量级――来补充。我完全相信本世纪的某一天,我们将发现类似受抑制重子的非守恒进程,使质子衰变成为粒子物理学家的主要关注点。
当然,在发现中微子质量的很久以前,我们知道除了标准模型外,还有别的理论提议新物理学的质量应稍稍超过1016 GeV:即引力的存在。还存在这样的事实,标准模型中仅同能量的对数相关的一个强耦合参数、两个电弱耦合参数,似乎在1015 GeV到1016 GeV能量级处汇合成了一个共同值。
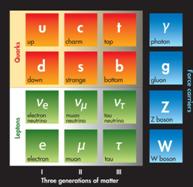
标准模型的基本粒子:此处显示的是三代夸克和轻子以及携带强相互作用力、电磁相互作用力和弱相互作用力的玻色子
关于超越标准模型,有许多很好的思路,包括超对称以及通常称之为弦理论的,但尚没有任何实验数据来验证它们。即使政府对粒子物理学慷慨程度超出了我们最疯狂的梦想,我们可能也永远无法建立可以达到如1015 GeV到1016 GeV能量的加速器。某一天我们可能会探测到极早期宇宙中膨胀时期发射的高频引力波,这可以告诉我们有关极高能量的物理进程。与此同时,我们可以期望LHC及其继任者将提供我们如此不顾一切想要的线索,以便超越以往100年的成功。
所有这一切价值何在?我们真的需要知道为什么有三代夸克和轻子,或大自然是否满足超对称性,或暗物质是什么吗?是的,我是这样认为。因为回答这类问题,就是学习过程的下一步,了解大自然是如何让所有的规律(一切皆非历史的偶然)遵循仅有的几条简单法则的。
在卢瑟福发现原子核后若干年里,这个过程一开始似乎可能与量子力学的出现有关。在那以前,化学被视为是建立在与物理学的原理相独立的原理之上的另一门科学――以致于本世纪初科学家们能对物理学滔滔不绝,然而却对从物理学中推断化学的原理无能为力。物理学家对此并不担心,因为解释化学现象似乎并非是他们的任务。但到了1929年,在量子力学获得发展之后,狄拉克宣布“基本物理定律对于物理学中大部分数学理论是必要的,而整个化学于是就必须完全了解。”
还原论者的计划――对所有科学原理追踪到几条简单的物理学法则――不仅是唯一重要的一种科学,甚至还是唯一重要的物理学,而且它还有其自身的特殊重要性,将在本世纪不断激励粒子物理学家前进。
现在一般认为,任何与量子力学和狭义相对论相协调的理论(连同“遥远的实验给出不相关的结果”的技术要求),将如量子场论那样考虑足够低的能量。在这种同无论是基本粒子还是非基本粒子对应的有效理论的场中,其质量小到足以在谈及的能量中产生。由于有效场论并非基本理论,我们没有理由期望它们要特别简单。恰恰相反,与假设对称性一致的有效理论的拉格朗日函数中,所有的无限多种可能的项将在理论中展现,每个项都各有其独立的系数。
这似乎可以是这样的理论,带有无限个自由参数,不会有多大的预测能力。有效理论在任何可以使一种相互作用更加复杂的情况下的效用,比如添加场因子或时空派生物的相互作用,将增加其维度(质量单位,以上η和c为单位)。在一个重整化理论中,所有拉格朗日函数项的维度必须小于等于4;这引起了本文中提到的简单化的条件。但在一个有效场论中,在拉格朗日密度函数中全部而数量有限的项的维度将大于4。从而这些复杂的项的系数必须令其与某些质量的次方成比例,因为拉格朗日密度函数本身其维度必须等于4。
如果有效场论产生于一个基础性的基本理论(或至少是一种更为基本的理论)中自由度“集成的”高能级,那么以高维相互作用尺度为特征的质量将成为基本理论中质量标度的级别。只要有效场论只是用于探索能量远低于这样的质量尺度,在有效场论中,微扰不取决于耦合常数,而是取决于基础性基本理论特有的质量尺度所分割的能量。
维度大于4的相互作用的出现,意味着有效场论无法在与量子电动力学相同意义上重整化。更确切地说,在超出了微扰理论的最低阶时,对于理论的有限个参数,不能通过重定义或重整化来取消发散积分。但这些无穷大的项可以通过在理论中重新定义无穷多的参数来消解。此外,在每一阶微扰理论,我们只会遇到有限数量的自由参数及有限数量的发散积分,后者的无穷大总可通过对那些自由参数重整化而消解。
粒子物理学中的有效场论首先应用在低能π介子的研究中,其基础的质量尺度约为1 GeV。低能π介子的有效理论也已扩展到能处理具有固定数目的原子核(原子核的质量不小于1 GeV,但这无关紧要,因为人们并不关心处理的是原子核的生成还是毁灭)。在π介子和原子核的有效场论中,本文提到的手征对称性不允许有任何的传统重整化的相互作用(即使用4维或少于4维的耦合常数)。
类似的,在引力的量子理论中,坐标选择不变性不允许任何引力的传统重整化相互作用。量子引力也是如此,已被视作一种有效场论。量子引力的问题不在于其无穷大,而是(如同在所有的有效理论中那样)它在充分高的能量下会失去所有预测力这个事实――此时,约为1019 GeV的普朗克尺度,或稍低。
老的费米β衰变理论可以被视为是4-费米子作用有效场论的一部分,只是在由100 GeV级的质量尺度划分的能量所确定的展开项中的首项,大约有W和Z玻色子的质量。在展开的下一阶我们会遇到发散积分,它可通过对少数新的4-费米子作用(包括某些原动力的额外因素)的重整化而变为有限。由于它的存在,在懂得如何将费米理论作为一个有效场论来使用之前,隐藏在费米理论中的理论就被发现。所谓隐藏的理论,自然指的是标准电弱理论,它允许在远高于100 GeV的能量上运用微扰理论,可一直达到1015 GeV。
资料来源 Physics Today
责任编辑 则 鸣
――――――――――
本文作者史蒂文·温伯格(Steven Weinberg),1979年诺贝尔物理学奖获得者,奥斯汀得克萨斯大学物理和天文系教授,理论物理小组负责人。本文是温伯格在美国物理学会2011年4月举行的“亚原子物理100年”研讨会上的发言,内容略有删改。
?相关链接?

物理学家寄希望于LHC能验证希格斯玻色子的存在
美国物理学家史蒂文·温伯格认为,在五六十年代粒子物理学产生了三个“出色的想法”:盖尔曼的夸克模型、杨振宁和罗伯特·米尔斯将规范对称性推广至非阿尔贝群(杨-米尔斯理论)来解释强相互作用、弱相互作用和自发对称性破缺(希格斯机制)。1967年,温伯格和阿卜杜勒·萨拉姆试图在杨-米尔斯理论基础上将规范场论应用到强相互作用,结果未果。后来温伯格在反思中发现可以将规范场论应用到格拉肖的弱电统一理论中,结果非常之成功,不仅能够给出矢量玻色子的质量,还能给出电子及其他轻子的质量。特别地,弱电统一理论还预言了一种可观测的粒子――希格斯玻色子。尽管迄今为止,关于希格斯玻色子仍然只凭经验性地间接认为其存在。
![]()




